 login/create account
login/create account
funcoid
Several ways to apply a (multivalued) multiargument function to a family of filters ★★★
Author(s): Porton
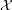 be an indexed family of filters on sets. Which of the below items are always pairwise equal?
be an indexed family of filters on sets. Which of the below items are always pairwise equal?
1. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the reloidal product of filters 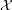 .
.
2. The funcoid corresponding to this function (considered as a single argument function on indexed families) applied to the starred reloidal product of filters 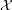 .
.
3. 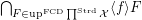 .
.
Keywords: funcoid; function; multifuncoid; staroid
Direct proof of a theorem about compact funcoids ★★
Author(s): Porton
 is a
is a 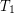 -separable (the same as
-separable (the same as 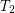 for symmetric transitive) compact funcoid and
for symmetric transitive) compact funcoid and 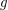 is a uniform space (reflexive, symmetric, and transitive endoreloid) such that
is a uniform space (reflexive, symmetric, and transitive endoreloid) such that 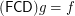 . Then
. Then 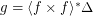 .
. The main purpose here is to find a direct proof of this conjecture. It seems that this conjecture can be derived from the well known theorem about existence of exactly one uniformity on a compact set. But that would be what I call an indirect proof, we need a direct proof instead.
The direct proof may be constructed by correcting all errors an omissions in this draft article.
Direct proof could be better because with it we would get a little more general statement like this:
 be a
be a 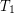 -separable compact reflexive symmetric funcoid and
-separable compact reflexive symmetric funcoid and 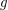 be a reloid such that
be a reloid such that- \item
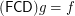 ; \item
; \item 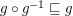 .
. Then 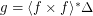 .
.
Keywords: compact space; compact topology; funcoid; reloid; uniform space; uniformity
Distributivity of a lattice of funcoids is not provable without axiom of choice ★
Author(s): Porton
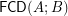 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets 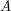 and
and 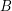 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice). A similar conjecture:
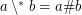 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice). Keywords: axiom of choice; distributive lattice; distributivity; funcoid; reverse math; reverse mathematics; ZF; ZFC
Distributivity of inward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; inward reloid; reloid
Reloid corresponding to funcoid is between outward and inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; outward reloid; reloid
Distributivity of union of funcoids corresponding to reloids ★★
Author(s): Porton
Keywords: funcoid; infinite distributivity; reloid
Inward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; inward reloid; reloid
Outward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; outward reloid; reloid
Distributivity of outward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; outward reloid; reloid
Funcoid corresponding to inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; reloid

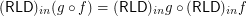 for any composable
for any composable ![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
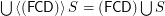 if
if 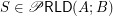 is a set of
is a set of 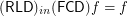 for any
for any 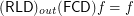 for any
for any 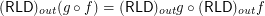 for any composable
for any composable 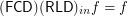 for any
for any  Drupal
Drupal CSI of Charles University
CSI of Charles University