 login/create account
login/create account
Reloid corresponding to funcoid is between outward and inward reloid (Solved)
See Algebraic General Topology for definitions of used concepts.
Counter-example: 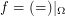 where
where 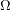 is the Frechet filter,
is the Frechet filter, 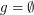 . Then
. Then 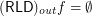 .
.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 and
and  having the same source and destination
having the same source and destination ![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
 Drupal
Drupal CSI of Charles University
CSI of Charles University
Please improve presentation!
Please, provide
1) definitions of the used concepts (to make the statement self-contained)
2) motivation (why this is important, examples, ...)
At the present state, this text is unfortunately not very useful for someone not acquainted with your manuscripts.