 login/create account
login/create account
compact topology
Direct proof of a theorem about compact funcoids ★★
Author(s): Porton
Conjecture Let  is a
is a 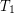 -separable (the same as
-separable (the same as 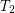 for symmetric transitive) compact funcoid and
for symmetric transitive) compact funcoid and  is a uniform space (reflexive, symmetric, and transitive endoreloid) such that
is a uniform space (reflexive, symmetric, and transitive endoreloid) such that 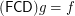 . Then
. Then 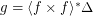 .
.
 is a
is a 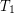 -separable (the same as
-separable (the same as 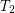 for symmetric transitive) compact funcoid and
for symmetric transitive) compact funcoid and  is a uniform space (reflexive, symmetric, and transitive endoreloid) such that
is a uniform space (reflexive, symmetric, and transitive endoreloid) such that 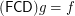 . Then
. Then 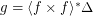 .
. The main purpose here is to find a direct proof of this conjecture. It seems that this conjecture can be derived from the well known theorem about existence of exactly one uniformity on a compact set. But that would be what I call an indirect proof, we need a direct proof instead.
The direct proof may be constructed by correcting all errors an omissions in this draft article.
Direct proof could be better because with it we would get a little more general statement like this:
Conjecture Let  be a
be a 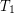 -separable compact reflexive symmetric funcoid and
-separable compact reflexive symmetric funcoid and  be a reloid such that
be a reloid such that
 be a
be a 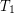 -separable compact reflexive symmetric funcoid and
-separable compact reflexive symmetric funcoid and  be a reloid such that
be a reloid such that- \item
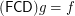 ; \item
; \item 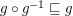 .
. Then 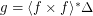 .
.
Keywords: compact space; compact topology; funcoid; reloid; uniform space; uniformity

 Drupal
Drupal CSI of Charles University
CSI of Charles University