 login/create account
login/create account
Conjecture Distributivity of the lattice 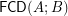 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 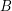 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice).
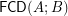 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 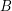 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice). A similar conjecture:
Conjecture 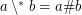 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice).
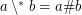 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice). See this blog post for a rationale of this conjecture.
See here for used notation.
The first conjecture is shown false (that is a proof without AC exists) by Todd Trimble.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University