 login/create account
login/create account
Recent Activity
Lindelöf hypothesis ★★
Author(s): Lindelöf
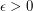
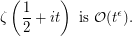
Since  can be replaced by a smaller value, we can also write the conjecture as, for any positive
can be replaced by a smaller value, we can also write the conjecture as, for any positive  ,
, 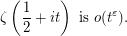
Keywords: Riemann Hypothesis; zeta
Termination of the sixth Goodstein Sequence ★
Author(s): Graham
Keywords: Goodstein Sequence
Consecutive non-orientable embedding obstructions ★★★
Author(s):
 that is a minor-minimal obstruction for two non-orientable surfaces?
that is a minor-minimal obstruction for two non-orientable surfaces? Diagonal Ramsey numbers ★★★★
Author(s): Erdos
Let 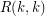 denote the
denote the 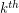 diagonal Ramsey number.
diagonal Ramsey number.
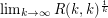 exists.
exists. Keywords: Ramsey number
The 4x5 chessboard complex is the complement of a link, which link? ★★
Author(s): David Eppstein
Keywords: knot theory, links, chessboard complex
Elementary symmetric of a sum of matrices ★★★
Author(s):
Given a Matrix  , the
, the  -th elementary symmetric function of
-th elementary symmetric function of  , namely
, namely 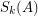 , is defined as the sum of all
, is defined as the sum of all  -by-
-by- principal minors.
principal minors.
Find a closed expression for the  -th elementary symmetric function of a sum of N
-th elementary symmetric function of a sum of N  -by-
-by- matrices, with
matrices, with 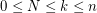 by using partitions.
by using partitions.
Keywords:
Monochromatic empty triangles ★★★
Author(s):
If 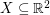 is a finite set of points which is 2-colored, an empty triangle is a set
is a finite set of points which is 2-colored, an empty triangle is a set 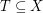 with
with 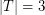 so that the convex hull of
so that the convex hull of  is disjoint from
is disjoint from  . We say that
. We say that  is monochromatic if all points in
is monochromatic if all points in  are the same color.
are the same color.
 with the following property. If
with the following property. If 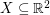 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 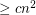 monochromatic empty triangles.
monochromatic empty triangles. Keywords: empty triangle; general position; ramsey theory
Edge-antipodal colorings of cubes ★★
Author(s): Norine
We let 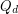 denote the
denote the  -dimensional cube graph. A map
-dimensional cube graph. A map 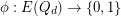 is called edge-antipodal if
is called edge-antipodal if 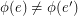 whenever
whenever 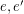 are antipodal edges.
are antipodal edges.
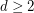 and
and 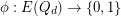 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 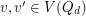 which are joined by a monochromatic path.
which are joined by a monochromatic path. Keywords: antipodal; cube; edge-coloring
Exponential Algorithms for Knapsack ★★
Author(s): Lipton
The famous 0-1 Knapsack problem is: Given 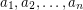 and
and  integers, determine whether or not there are
integers, determine whether or not there are 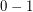 values
values 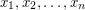 so that
so that 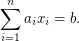 The best known worst-case algorithm runs in time
The best known worst-case algorithm runs in time 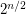 times a polynomial in
times a polynomial in  . Is there an algorithm that runs in time
. Is there an algorithm that runs in time 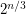 ?
?
Keywords: Algorithm construction; Exponential-time algorithm; Knapsack
Unsolvability of word problem for 2-knot complements ★★★
Author(s): Gordon
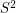 in
in 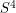 such that the fundamental group of the complement has an unsolvable word problem?
such that the fundamental group of the complement has an unsolvable word problem? Keywords: 2-knot; Computational Complexity; knot theory
Algorithm for graph homomorphisms ★★
Author(s): Fomin; Heggernes; Kratsch
Is there an algorithm that decides, for input graphs  and
and  , whether there exists a homomorphism from
, whether there exists a homomorphism from  to
to  in time
in time 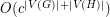 for some constant
for some constant  ?
?
Keywords: algorithm; Exponential-time algorithm; homomorphism
Exact colorings of graphs ★★
Author(s): Erickson
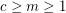 , let
, let 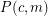 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 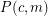 is true if and only if
is true if and only if 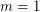 ,
, 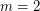 , or
, or  .
. Keywords: graph coloring; ramsey theory
Dividing up the unrestricted partitions ★★
Begin with the generating function for unrestricted partitions:
(1+x+x^2+...)(1+x^2+x^4+...)(1+x^3+x^6+...)...
Now change some of the plus signs to minus signs. The resulting series will have coefficients congruent, mod 2, to the coefficients of the generating series for unrestricted partitions. I conjecture that the signs may be chosen such that all the coefficients of the series are either 1, -1, or zero.
Keywords: congruence properties; partition
The stubborn list partition problem ★★
Author(s): Cameron; Eschen; Hoang; Sritharan
 and for every vertex
and for every vertex 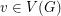 a subset
a subset 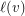 of
of 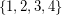 , and decides if there exists a partition of
, and decides if there exists a partition of 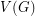 into
into 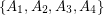 so that
so that 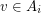 only if
only if 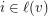 and so that
and so that 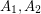 are independent,
are independent, 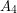 is a clique, and there are no edges between
is a clique, and there are no edges between 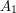 and
and 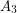 ?
? Keywords: list partition; polynomial algorithm
Long rainbow arithmetic progressions ★★
Author(s): Fox; Jungic; Mahdian; Nesetril; Radoicic
For 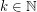 let
let 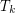 denote the minimal number
denote the minimal number 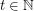 such that there is a rainbow
such that there is a rainbow 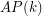 in every equinumerous
in every equinumerous  -coloring of
-coloring of 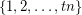 for every
for every 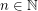
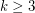 ,
, 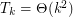 .
. Keywords: arithmetic progression; rainbow
Reconstruction conjecture ★★★★
The deck of a graph  is the multiset consisting of all unlabelled subgraphs obtained from
is the multiset consisting of all unlabelled subgraphs obtained from  by deleting a vertex in all possible ways (counted according to multiplicity).
by deleting a vertex in all possible ways (counted according to multiplicity).
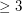 vertices have the same deck, then they are isomorphic.
vertices have the same deck, then they are isomorphic. Keywords: reconstruction
Finding k-edge-outerplanar graph embeddings ★★
Author(s): Bentz
 -outerplanar embedding for which
-outerplanar embedding for which  is minimal can be found in polynomial time. Does a similar result hold for
is minimal can be found in polynomial time. Does a similar result hold for  -edge-outerplanar graphs?
-edge-outerplanar graphs? Keywords: planar graph; polynomial algorithm
Approximation ratio for k-outerplanar graphs ★★
Author(s): Bentz
 -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs? Keywords: approximation algorithms; planar graph; polynomial algorithm
Approximation Ratio for Maximum Edge Disjoint Paths problem ★★
Author(s): Bentz
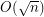 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 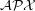 -hardness?
-hardness? Keywords: approximation algorithms; Disjoint paths; planar graph; polynomial algorithm
Beneš Conjecture (graph-theoretic form) ★★★
Author(s): Beneš
 ) Find a sufficient condition for a straight
) Find a sufficient condition for a straight 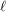 -stage graph to be rearrangeable. In particular, what about a straight uniform graph?
-stage graph to be rearrangeable. In particular, what about a straight uniform graph?  ) Let
) Let 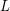 be a simple regular ordered
be a simple regular ordered  -stage graph. Suppose that the graph
-stage graph. Suppose that the graph 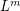 is externally connected, for some
is externally connected, for some 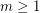 . Then the graph
. Then the graph 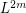 is rearrangeable.
is rearrangeable. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University