login/create account
Reconstruction conjecture
The deck of a graph 
is the multiset consisting of all unlabelled subgraphs obtained from by deleting a vertex in all possible ways (counted according to multiplicity).
Conjecture If two graphs on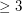 
vertices have the same deck, then they are isomorphic.
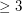vertices have the same deck, then they are isomorphic. See Wikipedia's Reconstruction Conjecture for more on this problem.
Bibliography
*[K] P. J. Kelly, A congruence theorem for trees, Pacific J. Math., 7 (1957), 961–968.
*[U] S. M. Ulam, A collection of mathematical problems, Wiley, New York, 1960.
* indicates original appearance(s) of problem.
correction and partial results
On May 23rd, 2008 melch says:
this should be on 3 or more vertices. False for digraphs, hypergraphs, and infinite graphs. It is open for simple graphs and multigraphs
Drupal
CSI of Charles University
A strategy for simple graphs?
How about 1) Prove for a 4-node, or tetrahedral graph. 2) Demonstrate that all graphs with > 4 nodes are composed of multiple overlapping tetrahedrons 3) Figure out how coupled tetrahedra function when nodes are deleted. 4) Induct on number of tetrahedra in graph. ?
Obviously (3) is the tough part, but why should it be impossible?