 login/create account
login/create account
arithmetic progression
Rainbow AP(4) in an almost equinumerous coloring ★★
Author(s): Conlon
Problem Do 4-colorings of 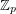 , for
, for  a large prime, always contain a rainbow
a large prime, always contain a rainbow 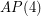 if each of the color classes is of size of either
if each of the color classes is of size of either 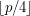 or
or 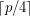 ?
?
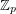 , for
, for  a large prime, always contain a rainbow
a large prime, always contain a rainbow 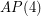 if each of the color classes is of size of either
if each of the color classes is of size of either 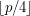 or
or 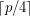 ?
? Keywords: arithmetic progression; rainbow
Long rainbow arithmetic progressions ★★
Author(s): Fox; Jungic; Mahdian; Nesetril; Radoicic
For 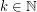 let
let 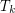 denote the minimal number
denote the minimal number 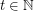 such that there is a rainbow
such that there is a rainbow 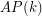 in every equinumerous
in every equinumerous  -coloring of
-coloring of 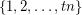 for every
for every 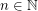
Conjecture For all 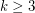 ,
, 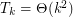 .
.
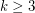 ,
, 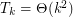 .
. Keywords: arithmetic progression; rainbow
Concavity of van der Waerden numbers ★★
Author(s): Landman
For  and
and  positive integers, the (mixed) van der Waerden number
positive integers, the (mixed) van der Waerden number 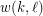 is the least positive integer
is the least positive integer  such that every (red-blue)-coloring of
such that every (red-blue)-coloring of ![$ [1,n] $](/files/tex/661d0acc09fbc5b62f49645a71cf7d831a26563f.png) admits either a
admits either a  -term red arithmetic progression or an
-term red arithmetic progression or an  -term blue arithmetic progression.
-term blue arithmetic progression.
Conjecture For all  and
and  with
with 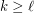 ,
, 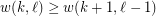 .
.
 and
and  with
with 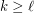 ,
, 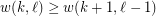 .
. Keywords: arithmetic progression; van der Waerden

 Drupal
Drupal CSI of Charles University
CSI of Charles University