 login/create account
login/create account
Beneš, Václav E.
Beneš Conjecture (graph-theoretic form) ★★★
Author(s): Beneš
 ) Find a sufficient condition for a straight
) Find a sufficient condition for a straight  -stage graph to be rearrangeable. In particular, what about a straight uniform graph?
-stage graph to be rearrangeable. In particular, what about a straight uniform graph?  ) Let
) Let  be a simple regular ordered
be a simple regular ordered 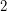 -stage graph. Suppose that the graph
-stage graph. Suppose that the graph 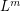 is externally connected, for some
is externally connected, for some 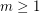 . Then the graph
. Then the graph 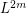 is rearrangeable.
is rearrangeable. Keywords:
Beneš Conjecture ★★★
Author(s): Beneš
Let  be a non-empty finite set. Given a partition
be a non-empty finite set. Given a partition 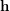 of
of  , the stabilizer of
, the stabilizer of 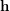 , denoted
, denoted 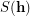 , is the group formed by all permutations of
, is the group formed by all permutations of  preserving each block of
preserving each block of 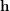 .
.
 ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 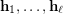 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 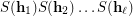 is equal to the whole symmetric group
is equal to the whole symmetric group 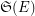 on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 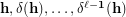 , given a partition
, given a partition 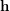 of
of  and a permutation
and a permutation  of
of  ?
? 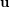 be a uniform partition of
be a uniform partition of  and
and 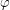 be a permutation of
be a permutation of  such that
such that 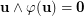 . Suppose that the set
. Suppose that the set 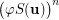 is transitive, for some integer
is transitive, for some integer 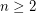 . Then
. Then 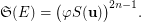
Keywords:
Shuffle-Exchange Conjecture ★★★
Author(s): Beneš; Folklore; Stone
Given integers 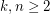 , let
, let 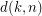 be the smallest integer
be the smallest integer  such that the symmetric group
such that the symmetric group 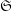 on the set of all words of length
on the set of all words of length  over a
over a  -letter alphabet can be generated as
-letter alphabet can be generated as 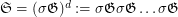 (
( times), where
times), where 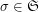 is the shuffle permutation defined by
is the shuffle permutation defined by 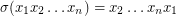 , and
, and 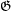 is the exchange group consisting of all permutations in
is the exchange group consisting of all permutations in 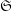 preserving the first
preserving the first 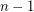 letters in the words.
letters in the words.
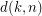 .
. 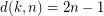 , for all
, for all 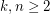 .
. Keywords:
Shuffle-Exchange Conjecture (graph-theoretic form) ★★★
Author(s): Beneš; Folklore; Stone
Given integers 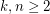 , the 2-stage Shuffle-Exchange graph/network, denoted
, the 2-stage Shuffle-Exchange graph/network, denoted 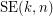 , is the simple
, is the simple  -regular bipartite graph with the ordered pair
-regular bipartite graph with the ordered pair 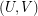 of linearly labeled parts
of linearly labeled parts 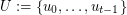 and
and 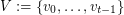 , where
, where 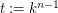 , such that vertices
, such that vertices 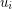 and
and 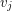 are adjacent if and only if
are adjacent if and only if  (see Fig.1).
(see Fig.1).
Given integers 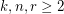 , the
, the  -stage Shuffle-Exchange graph/network, denoted
-stage Shuffle-Exchange graph/network, denoted 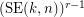 , is the proper (i.e., respecting all the orders) concatenation of
, is the proper (i.e., respecting all the orders) concatenation of 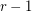 identical copies of
identical copies of 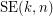 (see Fig.1).
(see Fig.1).
Let 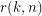 be the smallest integer
be the smallest integer 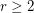 such that the graph
such that the graph 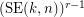 is rearrangeable.
is rearrangeable.
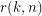 .
. 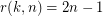 .
. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University