Home » Author index

Folklore


Theoretical Comp. Sci. » Complexity » Derandomization

P vs. BPP ★★★

Author(s): Folklore

Conjecture   Can all problems that can be computed by a probabilistic Turing machine (with error probability < 1/3) in polynomial time be solved by a deterministic Turing machine in polynomial time? That is, does P = BPP?

Keywords: BPP; circuit complexity; pseudorandom generators

Posted by Charles R Great...
updated June 14th, 2013
add new comment
Combinatorics

Shuffle-Exchange Conjecture ★★★

Author(s): Beneš; Folklore; Stone

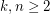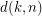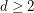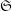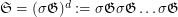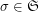Given integers $ k,n\ge2 $, let $ d(k,n) $ be the smallest integer $ d\ge2 $ such that the symmetric group $ \frak S $ on the set of all words of length $ n $ over a $ k $-letter alphabet can be generated as $ \frak S = (\sigma \frak G)^d:=\sigma\frak G \sigma\frak G \dots \sigma\frak G $ ($ d $ times), where $ \sigma\in \frak S $ is the shuffle permutation defined by 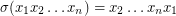$ \sigma(x_1 x_2 \dots x_{n}) = x_2 \dots x_{n} x_1 $, and $ \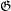frak G $ is the exchange group consisting of all permutations in 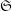$ \frak S $ preserving the first 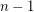$ n-1 $ letters in the words.

Problem  (SE)   Evaluate $ d(k,n) $.
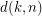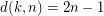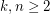Conjecture  (SE)   $ d(k,n)=2n-1 $, for all $ k,n\ge2 $.

Keywords:

Posted by Vadim Lioubimov
updated November 27th, 2009
add new comment
Graph Theory

Shuffle-Exchange Conjecture (graph-theoretic form) ★★★

Author(s): Beneš; Folklore; Stone

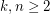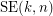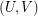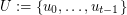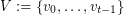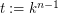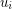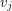Given integers $ k,n \ge 2 $, the 2-stage Shuffle-Exchange graph/network, denoted $ \text{SE}(k,n) $, is the simple $ k $-regular bipartite graph with the ordered pair $ (U,V) $ of linearly labeled parts $ U:=\{u_0,\dots,u_{t-1}\} $ and $ V:=\{v_0,\dots,v_{t-1}\} $, where $ t:=k^{n-1} $, such that vertices $ u_i $ and $ v_j $ are adjacent if and only if $ (j - ki) \text{ mod } t < k $ (see Fig.1).

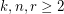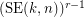Given integers $ k,n,r \ge 2 $, the $ r $-stage Shuffle-Exchange graph/network, denoted $ (\text{SE}(k,n))^{r-1} $, is the proper (i.e., respecting all the orders) concatenation of 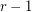$ r-1 $ identical copies of 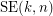$ \text{SE}(k,n) $ (see Fig.1).

Let 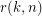$ r(k,n) $ be the smallest integer 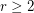$ r\ge 2 $ such that the graph 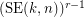$ (\text{SE}(k,n))^{r-1} $ is rearrangeable.

Problem   Find $ r(k,n) $.
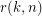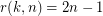Conjecture   $ r(k,n)=2n-1 $.

Keywords:

Posted by Vadim Lioubimov
updated October 30th, 2009
add new comment
Theoretical Comp. Sci. » Complexity

P vs. PSPACE ★★★

Author(s): Folklore

Problem   Is there a problem that can be computed by a Turing machine in polynomial space and unbounded time but not in polynomial time? More formally, does P = PSPACE?

Keywords: P; PSPACE; separation; unconditional

Posted by cwenner
updated April 4th, 2009
add new comment
Syndicate content