Home » Subject » Graph Theory
Importance: High ✭✭✭
Author(s): Beneš, Václav E.
Folklore
Stone, Harold S.
Subject: Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: Vadim Lioubimov
on: October 30th, 2009

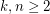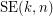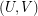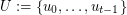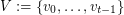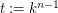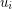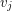Given integers $ k,n \ge 2 $, the 2-stage Shuffle-Exchange graph/network, denoted $ \text{SE}(k,n) $, is the simple $ k $-regular bipartite graph with the ordered pair $ (U,V) $ of linearly labeled parts $ U:=\{u_0,\dots,u_{t-1}\} $ and $ V:=\{v_0,\dots,v_{t-1}\} $, where $ t:=k^{n-1} $, such that vertices $ u_i $ and $ v_j $ are adjacent if and only if $ (j - ki) \text{ mod } t < k $ (see Fig.1).

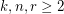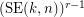Given integers $ k,n,r \ge 2 $, the $ r $-stage Shuffle-Exchange graph/network, denoted $ (\text{SE}(k,n))^{r-1} $, is the proper (i.e., respecting all the orders) concatenation of 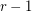$ r-1 $ identical copies of 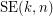$ \text{SE}(k,n) $ (see Fig.1).

Let 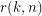$ r(k,n) $ be the smallest integer 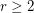$ r\ge 2 $ such that the graph 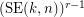$ (\text{SE}(k,n))^{r-1} $ is rearrangeable.

Problem   Find $ r(k,n) $.
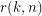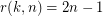Conjecture   $ r(k,n)=2n-1 $.

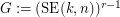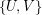A mask for the graph $ G:=(\text{SE}(k,n))^{r-1} $ is a $ k $-regular bipartite multigraph with the bipartition $ \{U,V\} $. The graph $ G $ is said to be rearrangeable if for every its mask there exists a collection, called routing, of corresponding mutually edge-disjoint paths in $ G $ connecting its end parts. (For simplicity, we do not provide here a more general definition for rearrangeability of graphs.)

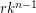Note that $ G $ is a simple $ r $-partite graph with $ r k^{n-1} $ vertices and 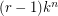$ (r-1)k^{n} $ edges, and any route for it consists exactly of 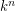$ k^{n} $ paths. Also, 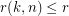$ r(k,n)\le r $ is equivalent to rearrangeability of $ G $.

Figure 1. Examples of multistage Shuffle-Exchange graphs.

For example, according to the conjecture, the graph 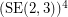$ (\text{SE}(2,3))^{4} $ (see Fig. 1) is rearrangeable, which is a well known result.

The problem and conjecture are equivalent "graph-theoretic" forms of remarkable Shuffle-Exchange (SE) problem and conjecture due to the following identity (that is not hard to show by normal reasoning):

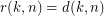Theorem   $ r(k,n)=d(k,n) $.

The definition of 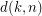$ d(k,n) $ and more on SE problem/conjecture including the other 2 main forms of them, combinatorial and group-theoretic, and a survey of results can be found here.

Related problems

Shuffle-Exchange Conjecture
Beneš Conjecture (graph-theoretic form)
Beneš Conjecture

Bibliography

*[S71] H.S. Stone, Parallel processing with the perfect shuffle, IEEE Trans. on Computers C-20 (1971), 153-161.

*[B75] V.E. Beneš, Proving the rearrangeability of connecting networks by group calculation, Bell Syst. Tech. J. 54 (1975), 421-434.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options