 login/create account
login/create account
Termination of the sixth Goodstein Sequence
For a positive integer  , the
, the 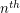 Goodstein Sequence is defined as follows. The first term of the sequence in
Goodstein Sequence is defined as follows. The first term of the sequence in  . To obtain the
. To obtain the 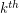 term, write the
term, write the 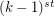 term in hereditary base k notation, change all
term in hereditary base k notation, change all  's to
's to 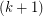 's and then subtract 1. If the sequence hits 0, then it terminates. So, the first terms of the sixth Goodstein Sequence are as follows:
's and then subtract 1. If the sequence hits 0, then it terminates. So, the first terms of the sixth Goodstein Sequence are as follows:
![\[ \begin{array}{lll} \mbox{term} & \mbox{value} <br> 1 & 2^2 + 2 = 6<br> 2 & 3^3 + 2 = 29<br> 3 & 4^4 + 1 = 257 <br> 4 & 5^5 = 3125 <br> 5 & 5 \cdot 6^5 + 5 \cdot 6^5 + 5 \cdot 6^4 + 5 \cdot 6^3 + 5 \cdot 6^2 + 5 \cdot 6 + 5 = 46655 \end{array} \]](/files/tex/d4e09812e648da3e7d8c9c3a89568081c5d5ed74.png)
Surprisingly, despite the fact that Goodstein Sequences grow quite quickly at the start, all such sequences do eventually hit 0 and terminate. This result, first discovered by Goodstein, is of interest in logic since it cannot be proved in Peano arithmetic.
Although determining particular properties of a specific Goodstein Sequence are of limited mathematical value, this problem is an interesting computational challenge.
Bibliography
* indicates original appearance(s) of problem.
The actual value is much higher
You've underestimated the true value by quite bit.
To get the value of the Goodstein function at n, you take n, write it in hereditary base 2, then replace every appearance to with the infinite ordinal  . Call the result R(n). The value of G(n) is then
. Call the result R(n). The value of G(n) is then 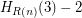 where
where 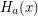 is the Hardy hierarchy, defined by
is the Hardy hierarchy, defined by
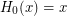
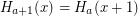
![$ H_a (x) = H_{a[x]} (x) $](/files/tex/e502999c62964754a8d9df317ca19ccc6ca6ca5d.png) for limit ordinals a
for limit ordinals a
So to find G(6), we write 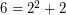 , so
, so 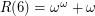 . Hence,
. Hence, 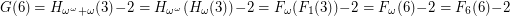
where 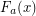 is the fast-growing hierarchy, defined by
is the fast-growing hierarchy, defined by
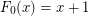
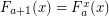
![$ F_a (x) = F_{a[x]} (x) $](/files/tex/515e55fd9531794926a0bf786b2e51ba3598dc55.png) for limit ordinals a
for limit ordinals a
(or you could just leave the answer in terms of the Hardy hierarchy, I just changed to the fast-growing hierarchy because the answer is a little simpler.)
Solution
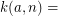 amount of steps to reduce
amount of steps to reduce 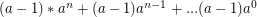 to -1
to -1
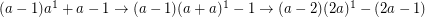
If you do this a - 1 times: 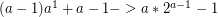
Which means it is reduced to a 0th power and will take 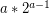 steps to finish.
steps to finish.
So total steps 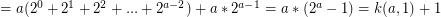
For 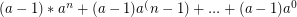 :
:
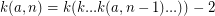 [k a times]
[k a times]
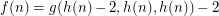
Where 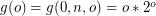 ,
, 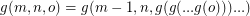 [n copies of g] and
[n copies of g] and 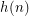 is the first number in the sequence in the form
is the first number in the sequence in the form 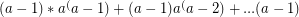
![$ h([3,4,5,6,7])=[2, 3, 4, 6, 8] $](/files/tex/fa7055371efcb41806f19c1c3bff51f2799ccd1c.png)
E.g.
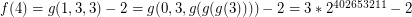
Using 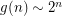 :
:
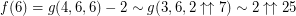
Has this solution been
Has this solution been verified by the author? Just curious.
Nah, I just posted it here
Nah, I just posted it here as my attempt at a solution. It probably needs to be done a bit better, but I believe it works until n = 8 or so, where you have to do a bit extra. I might try make it a bit clearer and rigorous at some point. Plus a better approximation would be useful.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
approximate value
So how much is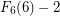 in terms of, say, Knuth arrows? we have
in terms of, say, Knuth arrows? we have 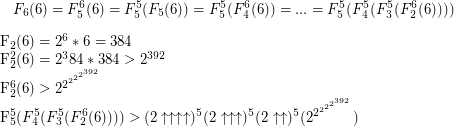 That's about as close an approximation as you can get.
That's about as close an approximation as you can get.