Home ยป Termination of the sixth Goodstein Sequence

approximate value

On September 17th, 2010 Deedlit says:

So how much is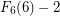 $ F_6(6) - 2 $ in terms of, say, Knuth arrows? we have 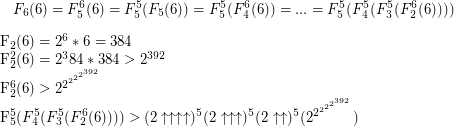$$ F_6(6) = F_5^6(6) = F_5^5(F_5(6)) = F_5^5(F_4^6(6)) = ... = F_5^5(F_4^5(F_3^5(F_2^6(6))))</p> <p>F_2(6) = 2^6*6 = 384</p> <p>F_2^2(6) = 2^384 * 384 > 2^{392}</p> <p>F_2^6(6) > 2^{2^{2^{2^{2^{392}}}}}</p> <p>F_5^5(F_4^5(F_3^5(F_2^6(6)))) > (2\uparrow\uparrow\uparrow\uparrow)^5 (2\uparrow\uparrow\uparrow)^5 (2\uparrow\uparrow)^5 (2^{2^{2^{2^{2^{392}}}}}) $$ That's about as close an approximation as you can get.

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options