amount of steps to reduce to -1
If you do this a - 1 times:
Which means it is reduced to a 0th power and will take steps to finish.
So total steps
For :
[k a times]
Where , [n copies of g] and is the first number in the sequence in the form
E.g.
Using :
Solution
If you do this a - 1 times: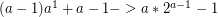
Which means it is reduced to a 0th power and will take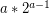 steps to finish.
steps to finish.
So total steps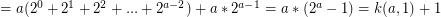
For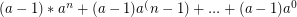 :
:
Where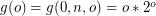 ,
, 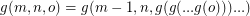 [n copies of g] and
[n copies of g] and 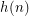 is the first number in the sequence in the form
is the first number in the sequence in the form 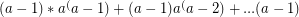
![$ h([3,4,5,6,7])=[2, 3, 4, 6, 8] $](/files/tex/fa7055371efcb41806f19c1c3bff51f2799ccd1c.png)
E.g.
Using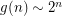 :
: