You've underestimated the true value by quite bit.
To get the value of the Goodstein function at n, you take n, write it in hereditary base 2, then replace every appearance to with the infinite ordinal . Call the result R(n). The value of G(n) is then where is the Hardy hierarchy, defined by
for limit ordinals a
So to find G(6), we write , so . Hence,
where is the fast-growing hierarchy, defined by
for limit ordinals a
(or you could just leave the answer in terms of the Hardy hierarchy, I just changed to the fast-growing hierarchy because the answer is a little simpler.)
The actual value is much higher
You've underestimated the true value by quite bit.
To get the value of the Goodstein function at n, you take n, write it in hereditary base 2, then replace every appearance to with the infinite ordinal . Call the result R(n). The value of G(n) is then
. Call the result R(n). The value of G(n) is then 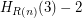 where
where 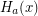 is the Hardy hierarchy, defined by
is the Hardy hierarchy, defined by
So to find G(6), we write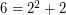 , so
, so 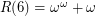 . Hence,
. Hence, 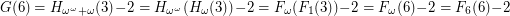
where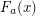 is the fast-growing hierarchy, defined by
is the fast-growing hierarchy, defined by
(or you could just leave the answer in terms of the Hardy hierarchy, I just changed to the fast-growing hierarchy because the answer is a little simpler.)