 login/create account
login/create account
Recent Activity
Sequence defined on multisets ★★
Author(s): Erickson
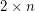 array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array
array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) , the sequence is:
, the sequence is: ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) ->
-> ![$ [1; 2] $](/files/tex/83c3d9d7589f716ed6b0f05d26d36dabe8ba47aa.png) ->
-> ![$ [1, 2; 1, 1] $](/files/tex/a6a696aec4e84df6bc046cf6d30a4df80e156a14.png) ->
-> ![$ [1, 2; 3, 1] $](/files/tex/98b2f3e4134422c8a286f0326fc2f57ca9be2ab7.png) ->
-> ![$ [1, 2, 3; 2, 1, 1] $](/files/tex/19a9d24510f4551fa45b950aed32efed0636b355.png) ->
-> ![$ [1, 2, 3; 3, 2, 1] $](/files/tex/b00d573110ba8c2472820409103dd4cbd7bff7cc.png) ->
-> ![$ [1, 2, 3; 2, 2, 2] $](/files/tex/2aae90b65ae3f116402a1c0143127f80d86acdf0.png) ->
-> ![$ [1, 2, 3; 1, 4, 1] $](/files/tex/d614399c4078a70fbffb24eb99816a0974423175.png) ->
-> ![$ [1, 2, 3, 4; 3, 1, 1, 1] $](/files/tex/bf4dd82eaf95bd71a88cb78d3367efa2c7e4c942.png) ->
-> ![$ [1, 2, 3, 4; 4, 1, 2, 1] $](/files/tex/a4ef5900a9dde9b32311afe7dee2b143f42c405f.png) ->
-> ![$ [1, 2, 3, 4; 3, 2, 1, 2] $](/files/tex/ff367376ed7bb74fc6207273d7157062b83a1be6.png) ->
-> ![$ [1, 2, 3, 4; 2, 3, 2, 1] $](/files/tex/81ba2b3608ddba2fc95d32b74b70279f3f5adc5b.png) , and we now have a fixed point (loop of one array).
, and we now have a fixed point (loop of one array).
The process always results in a loop of 1, 2, or 3 arrays.
Vertex Coloring of graph fractional powers ★★★
Author(s): Iradmusa
 be a graph and
be a graph and  be a positive integer. The
be a positive integer. The 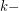 power of
power of  , denoted by
, denoted by 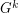 , is defined on the vertex set
, is defined on the vertex set 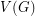 , by connecting any two distinct vertices
, by connecting any two distinct vertices  and
and 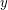 with distance at most
with distance at most  . In other words,
. In other words, 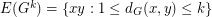 . Also
. Also 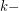 subdivision of
subdivision of  , denoted by
, denoted by 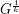 , is constructed by replacing each edge
, is constructed by replacing each edge 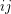 of
of  with a path of length
with a path of length  . Note that for
. Note that for 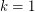 , we have
, we have 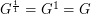 .
.Now we can define the fractional power of a graph as follows:
Let
 be a graph and
be a graph and 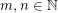 . The graph
. The graph 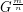 is defined by the
is defined by the 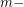 power of the
power of the 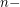 subdivision of
subdivision of  . In other words
. In other words 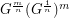 .
.Conjecture. Let
 be a connected graph with
be a connected graph with 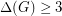 and
and  be a positive integer greater than 1. Then for any positive integer
be a positive integer greater than 1. Then for any positive integer 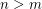 , we have
, we have 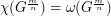 .
.In [1], it was shown that this conjecture is true in some special cases.
Keywords: chromatic number, fractional power of graph, clique number
Covering powers of cycles with equivalence subgraphs ★
Author(s):
 and
and  , the graph
, the graph 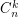 has equivalence covering number
has equivalence covering number 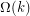 .
. Keywords:
Complexity of square-root sum ★★
Author(s): Goemans
Given 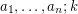 , determine whether or not
, determine whether or not 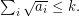
Keywords: semi-definite programming
Snevily's conjecture ★★★
Author(s): Snevily
 be an abelian group of odd order and let
be an abelian group of odd order and let 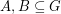 satisfy
satisfy 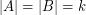 . Then the elements of
. Then the elements of  and
and 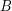 may be ordered
may be ordered 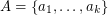 and
and 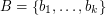 so that the sums
so that the sums 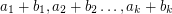 are pairwise distinct.
are pairwise distinct. Keywords: addition table; latin square; transversal
3-flow conjecture ★★★
Author(s): Tutte
Keywords: nowhere-zero flow
Invariant subspace problem ★★★
Author(s):
Keywords: subspace
Sets with distinct subset sums ★★★
Author(s): Erdos
Say that a set 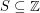 has distinct subset sums if distinct subsets of
has distinct subset sums if distinct subsets of  have distinct sums.
have distinct sums.
 so that
so that 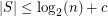 whenever
whenever 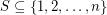 has distinct subset sums.
has distinct subset sums. Keywords: subset sum
Seymour's Second Neighbourhood Conjecture ★★★
Author(s): Seymour
Keywords: Caccetta-Häggkvist; neighbourhood; second; Seymour
Which lattices occur as intervals in subgroup lattices of finite groups? ★★★★
Author(s):
There exists a finite lattice that is not an interval in the subgroup lattice of a finite group.
Keywords: congruence lattice; finite groups
Quartic rationally derived polynomials ★★★
Author(s): Buchholz; MacDougall
Call a polynomial ![$ p \in {\mathbb Q}[x] $](/files/tex/a72fcb0a006c3c2afb3ba69722ccdb2599b83e90.png) rationally derived if all roots of
rationally derived if all roots of  and the nonzero derivatives of
and the nonzero derivatives of  are rational.
are rational.
![$ p \in {\mathbb Q}[x] $](/files/tex/a72fcb0a006c3c2afb3ba69722ccdb2599b83e90.png) with four distinct roots.
with four distinct roots. Keywords: derivative; diophantine; elliptic; polynomial
Nonseparating planar continuum ★★
Author(s):
A set has the fixed point property if every continuous map from it into itself has a fixed point.
Keywords: fixed point
Hilbert-Smith conjecture ★★
Author(s): David Hilbert; Paul A. Smith
 be a locally compact topological group. If
be a locally compact topological group. If  has a continuous faithful group action on an
has a continuous faithful group action on an  -manifold, then
-manifold, then  is a Lie group.
is a Lie group. Keywords:
trace inequality ★★
Author(s):
Let 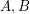 be positive semidefinite, by Jensen's inequality, it is easy to see
be positive semidefinite, by Jensen's inequality, it is easy to see ![$ [tr(A^s+B^s)]^{\frac{1}{s}}\leq [tr(A^r+B^r)]^{\frac{1}{r}} $](/files/tex/f5fa90ccf8c1dde9b9bf1f21399b3b5428dab81d.png) , whenever
, whenever 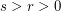 .
.
What about the 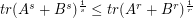 , is it still valid?
, is it still valid?
Keywords:
Real roots of the flow polynomial ★★
Author(s): Welsh
Keywords: flow polynomial; nowhere-zero flow
Hamiltonicity of Cayley graphs ★★★
Author(s): Rapaport-Strasser
Keywords:
Finite Lattice Representation Problem ★★★★
Author(s):
There exists a finite lattice which is not the congruence lattice of a finite algebra.
Keywords: congruence lattice; finite algebra
Outer reloid of restricted funcoid ★★
Author(s): Porton
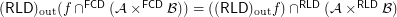 for every filter objects
for every filter objects 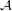 and
and 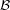 and a funcoid
and a funcoid 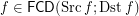 ?
? Keywords: direct product of filters; outer reloid
Star chromatic index of complete graphs ★★
Author(s): Dvorak; Mohar; Samal
 using
using 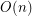 colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
colors, so that the coloring is proper and no 4-cycle and no 4-edge path is using only two colors?
Equivalently: is the star chromatic index of  linear in
linear in  ?
?
Keywords: complete graph; edge coloring; star coloring
Star chromatic index of cubic graphs ★★
Author(s): Dvorak; Mohar; Samal
The star chromatic index 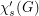 of a graph
of a graph  is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.
 , we have
, we have 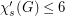 ?
? Keywords: edge coloring; star coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University