 login/create account
login/create account
chromatic number, fractional power of graph, clique number
Vertex Coloring of graph fractional powers ★★★
Author(s): Iradmusa
Conjecture Let  be a graph and
be a graph and  be a positive integer. The
be a positive integer. The 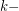 power of
power of  , denoted by
, denoted by 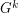 , is defined on the vertex set
, is defined on the vertex set 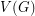 , by connecting any two distinct vertices
, by connecting any two distinct vertices  and
and 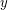 with distance at most
with distance at most  . In other words,
. In other words, 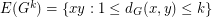 . Also
. Also 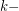 subdivision of
subdivision of  , denoted by
, denoted by 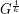 , is constructed by replacing each edge
, is constructed by replacing each edge 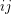 of
of  with a path of length
with a path of length  . Note that for
. Note that for 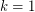 , we have
, we have 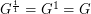 .
.
Now we can define the fractional power of a graph as follows:
Let be a graph and
be a graph and 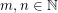 . The graph
. The graph 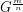 is defined by the
is defined by the 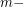 power of the
power of the 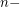 subdivision of
subdivision of  . In other words
. In other words 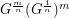 .
.
Conjecture. Let be a connected graph with
be a connected graph with 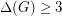 and
and  be a positive integer greater than 1. Then for any positive integer
be a positive integer greater than 1. Then for any positive integer 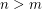 , we have
, we have 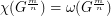 .
.
In [1], it was shown that this conjecture is true in some special cases.
 be a graph and
be a graph and  be a positive integer. The
be a positive integer. The 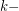 power of
power of  , denoted by
, denoted by 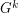 , is defined on the vertex set
, is defined on the vertex set 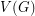 , by connecting any two distinct vertices
, by connecting any two distinct vertices  and
and 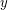 with distance at most
with distance at most  . In other words,
. In other words, 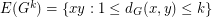 . Also
. Also 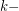 subdivision of
subdivision of  , denoted by
, denoted by 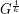 , is constructed by replacing each edge
, is constructed by replacing each edge 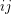 of
of  with a path of length
with a path of length  . Note that for
. Note that for 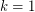 , we have
, we have 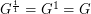 .
.Now we can define the fractional power of a graph as follows:
Let
 be a graph and
be a graph and 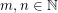 . The graph
. The graph 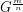 is defined by the
is defined by the 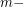 power of the
power of the 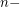 subdivision of
subdivision of  . In other words
. In other words 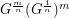 .
.Conjecture. Let
 be a connected graph with
be a connected graph with 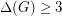 and
and  be a positive integer greater than 1. Then for any positive integer
be a positive integer greater than 1. Then for any positive integer 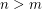 , we have
, we have 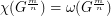 .
.In [1], it was shown that this conjecture is true in some special cases.
Keywords: chromatic number, fractional power of graph, clique number

 Drupal
Drupal CSI of Charles University
CSI of Charles University