 login/create account
login/create account
trace inequality
Let 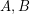 be positive semidefinite, by Jensen's inequality, it is easy to see
be positive semidefinite, by Jensen's inequality, it is easy to see ![$ [tr(A^s+B^s)]^{\frac{1}{s}}\leq [tr(A^r+B^r)]^{\frac{1}{r}} $](/files/tex/f5fa90ccf8c1dde9b9bf1f21399b3b5428dab81d.png) , whenever
, whenever 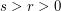 .
.
What about the 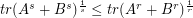 , is it still valid?
, is it still valid?
Bibliography
* indicates original appearance(s) of problem.
this inequality is not true.
On December 20th, 2010 Anonymous says:
this inequality is not true. It was denied some years ago. See X.Z Zhan's

 Drupal
Drupal CSI of Charles University
CSI of Charles University
clarification
I suppose that A and B are square hermitian matrixes and that s and r are real numbers. But what are the brackets supposed to represent? Sorry for my ignorance if it is obvious.