 login/create account
login/create account
Let 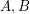 be positive semidefinite, by Jensen's inequality, it is easy to see
be positive semidefinite, by Jensen's inequality, it is easy to see ![$ [tr(A^s+B^s)]^{\frac{1}{s}}\leq [tr(A^r+B^r)]^{\frac{1}{r}} $](/files/tex/f5fa90ccf8c1dde9b9bf1f21399b3b5428dab81d.png) , whenever
, whenever 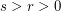 .
.
What about the 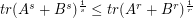 , is it still valid?
, is it still valid?
Bibliography
* indicates original appearance(s) of problem.
| Recomm. for undergrads: no |
| Posted | by: | Miwa Lin |
| on: | October 11th, 2008 |
Let 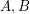 be positive semidefinite, by Jensen's inequality, it is easy to see
be positive semidefinite, by Jensen's inequality, it is easy to see ![$ [tr(A^s+B^s)]^{\frac{1}{s}}\leq [tr(A^r+B^r)]^{\frac{1}{r}} $](/files/tex/f5fa90ccf8c1dde9b9bf1f21399b3b5428dab81d.png) , whenever
, whenever 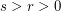 .
.
What about the 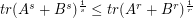 , is it still valid?
, is it still valid?