Home » Subject » Graph Theory
Importance: Low ✭
Author(s):
Subject: Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: Andrew King
on: July 7th, 2011
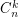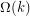Conjecture   Given $ k $ and $ n $, the graph $ C_{n}^k $ has equivalence covering number $ \Omega(k) $.

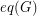Given a graph $ G $, a subgraph $ H $ of $ G $ is an equivalence subgraph of $ G $ if $ H $ a disjoint union of cliques. The quivalence covering number of $ G $, denoted $ eq(G) $, is the least number of equivalence subgraphs needed to cover the edges of $ G $.

This problem has been studied by various people since the 80s [A]. For line graphs, the equivalence covering number is known to within a constant factor [EGK]. It is therefore tempting to examine the situation for quasi-line graphs and claw-free graphs. Powers of cycles are perhaps the simplest interesting class of claw-free graphs that are not necessarily line graphs. 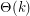However, even for $ n $ very large compared to $ k $, no upper bound is known beyond trivial linear bounds of order $ \Theta(k) $. Furthermore, it is not even certain that a nontrivial lower bound (i.e. going to infinity as $ k $ goes to infinity) is known. It is possible that this can be related somehow to a known result, but for now it seems at least superficially that this problem is wide open.

Bibliography

[A] N. Alon, Covering graphs with the minimum number of equivalence relations, Combinatorica 6 (1986) 201–206.

[EGK] L. Esperet, J. Gimbel, A. King, Covering line graphs with equivalence relations, Discrete Applied Mathematics Volume 158, Issue 17, 28 October 2010, Pages 1902-1907.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options