 login/create account
login/create account
Conjecture For 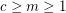 , let
, let 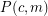 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 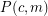 is true if and only if
is true if and only if 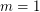 ,
, 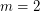 , or
, or  .
.
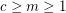 , let
, let 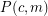 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 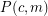 is true if and only if
is true if and only if 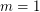 ,
, 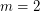 , or
, or  .
. Stacey and Weidl have shown that given 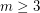 , there is an integer
, there is an integer 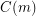 such that
such that 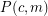 is false for all
is false for all 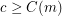 .
.
Bibliography
* M. Erickson, ``A Conjecture Concerning Ramsey's Theorem,'' Discrete Mathematics 126, 395--398 (1994); MR 95b:05209
A. Stacey and P. Weidl, "The Existence of Exactly m-Coloured Complete Subgraphs," J. of Combinatorial Theory, Series B 75, 1-18 (1999)
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University