 login/create account
login/create account
geometric graph
Circular colouring the orthogonality graph ★★
Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr
Let 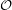 denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 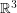 and two vertices adjacent in
and two vertices adjacent in 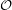 if they are perpendicular.
if they are perpendicular.
Problem Is 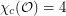 ?
?
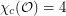 ?
? Keywords: circular coloring; geometric graph; orthogonality
Coloring the Odd Distance Graph ★★★
Author(s): Rosenfeld
The Odd Distance Graph, denoted 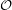 , is the graph with vertex set
, is the graph with vertex set  and two points adjacent if the distance between them is an odd integer.
and two points adjacent if the distance between them is an odd integer.
Question Is 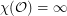 ?
?
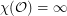 ?
? Keywords: coloring; geometric graph; odd distance
Universal point sets for planar graphs ★★★
Author(s): Mohar
We say that a set 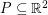 is
is  -universal if every
-universal if every  vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in
vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in  , and all edges are (non-intersecting) straight line segments.
, and all edges are (non-intersecting) straight line segments.
Question Does there exist an  -universal set of size
-universal set of size 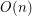 ?
?
 -universal set of size
-universal set of size 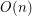 ?
? Keywords: geometric graph; planar graph; universal set

 Drupal
Drupal CSI of Charles University
CSI of Charles University