 login/create account
login/create account
Azarija, Jernej
Minimal graphs with a prescribed number of spanning trees ★★
Author(s): Azarija; Skrekovski
Conjecture Let 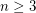 be an integer and let
be an integer and let 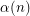 denote the least integer
denote the least integer  such that there exists a simple graph on
such that there exists a simple graph on  vertices having precisely
vertices having precisely  spanning trees. Then
spanning trees. Then 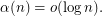
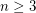 be an integer and let
be an integer and let 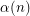 denote the least integer
denote the least integer  such that there exists a simple graph on
such that there exists a simple graph on  vertices having precisely
vertices having precisely  spanning trees. Then
spanning trees. Then 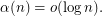
Keywords: number of spanning trees, asymptotics

 Drupal
Drupal CSI of Charles University
CSI of Charles University