 login/create account
login/create account
Minimal graphs with a prescribed number of spanning trees
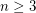 be an integer and let
be an integer and let 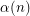 denote the least integer
denote the least integer  such that there exists a simple graph on
such that there exists a simple graph on  vertices having precisely
vertices having precisely  spanning trees. Then
spanning trees. Then 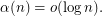
Observe that 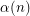 is well defined for
is well defined for 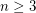 since
since 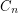 has
has  spanning trees.
spanning trees.
The function was introduced by Sedlacek [S] who has shown that for large enough 
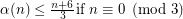 and
and 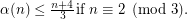
Using the fact that almost all positive integers  are expressible as
are expressible as 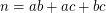 for integers
for integers  it can be shown [A] that for large enough
it can be shown [A] that for large enough 
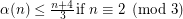 and
and 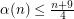 otherwise.
otherwise.
Moreover, the only fixed points of  are 3, 4, 5, 6, 7, 10, 13 and 22.
are 3, 4, 5, 6, 7, 10, 13 and 22.
The conjecture is motivated by the following graph (ploted for a very small sample of vertices)
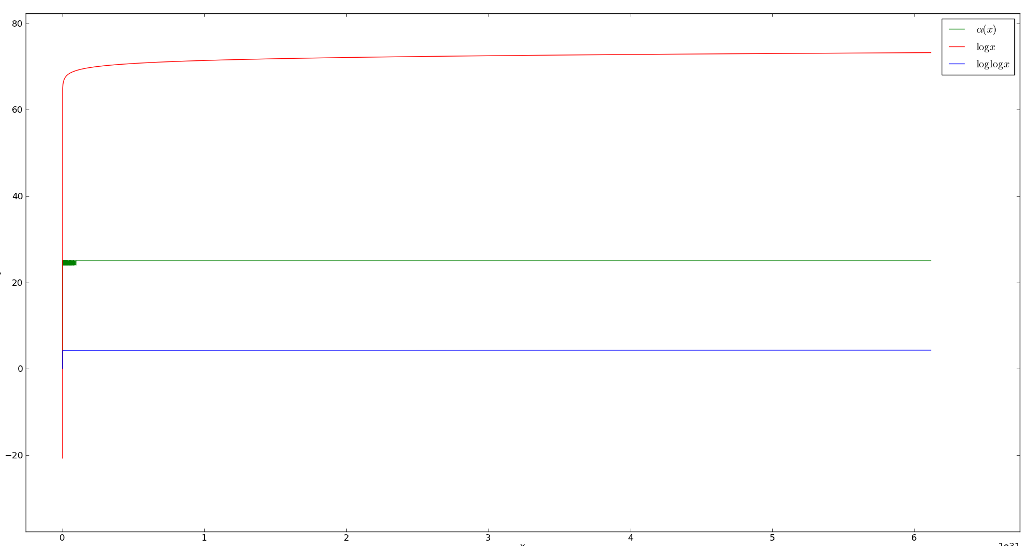
The conjecture [C] is justifiable for highly composite numbers  since in this case one can construct the graph obtained after taking cycles
since in this case one can construct the graph obtained after taking cycles 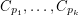 for every odd prime factor
for every odd prime factor 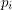 of
of  .
.
Bibliography
[S] J. Sedlacek, On the minimal graph with a given number of spanning trees, Canad. Math. Bull. 13 (1970) 515-517.
[A] J. Azarija, R. Skrekovski, Euler's idoneal numbers and an inequality concerning minimal graphs with a prescribed number of spanning trees, IMFM preprints 49 (2011) Link to paper
* [C] Minimal graphs with a prescribed number of spanning trees
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University