 login/create account
login/create account
Recent Activity
Alexa's Conjecture on Primality ★★
Author(s): Alexa
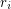 be the unique integer (with respect to a fixed
be the unique integer (with respect to a fixed 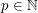 ) such that
) such that
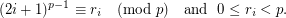
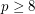 is a prime iff
is a prime iff ![$$ \displaystyle \sum_{i=1}^{\left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor} r_i = \left \lfloor \frac{\sqrt[3]p}{2} \right \rfloor $$](/files/tex/99af565f4cc4d3bab11eb3fbf54f78626678d484.png)
Keywords: primality
P vs. BPP ★★★
Author(s): Folklore
Keywords: BPP; circuit complexity; pseudorandom generators
Goldbach conjecture ★★★★
Author(s): Goldbach
Keywords: additive basis; prime
Goldberg's conjecture ★★★
Author(s): Goldberg
The overfull parameter is defined as follows: ![\[ w(G) = \max_{H \subseteq G} \left\lceil \frac{ |E(H)| }{ \lfloor \tfrac{1}{2} |V(H)| \rfloor} \right\rceil. \]](/files/tex/d2391343543ce03d861e6eb2f4985d52e309525d.png)
 satisfies
satisfies 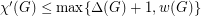 .
. Keywords: edge-coloring; multigraph
Cyclic spanning subdigraph with small cyclomatic number ★★
Author(s): Bondy
 be a digraph all of whose strong components are nontrivial. Then
be a digraph all of whose strong components are nontrivial. Then  contains a cyclic spanning subdigraph with cyclomatic number at most
contains a cyclic spanning subdigraph with cyclomatic number at most 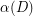 .
. Keywords:
inverse of an integer matrix ★★
Author(s): Gregory
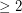 . Suppose X is an m-by-n integer matrix
. Suppose X is an m-by-n integer matrix 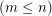 . Consider the partitioned matrix M = [D X]. Obviously M has full row rank so it has a right inverse of rational numbers. The question is, under what conditions does it have an integer right inverse? My guess, which I can't prove, is that the integers in each row need to be relatively prime.
. Consider the partitioned matrix M = [D X]. Obviously M has full row rank so it has a right inverse of rational numbers. The question is, under what conditions does it have an integer right inverse? My guess, which I can't prove, is that the integers in each row need to be relatively prime.
Keywords: invertable matrices, integer matrices
Minimum number of arc-disjoint transitive subtournaments of order 3 in a tournament ★★
Author(s): Yuster
 is a tournament of order
is a tournament of order  , then it contains
, then it contains 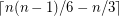 arc-disjoint transitive subtournaments of order 3.
arc-disjoint transitive subtournaments of order 3. Keywords:
Arc-disjoint directed cycles in regular directed graphs ★★
Author(s): Alon; McDiarmid; Molloy
 is a
is a  -regular directed graph with no parallel arcs, then
-regular directed graph with no parallel arcs, then  contains a collection of
contains a collection of 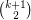 arc-disjoint directed cycles.
arc-disjoint directed cycles. Keywords:
Jacob Palis Conjecture(Finitude of Attractors)(Dynamical Systems) ★★★★
Author(s):
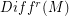 be the space of
be the space of 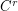 Diffeomorphisms on the connected , compact and boundaryles manifold M and
Diffeomorphisms on the connected , compact and boundaryles manifold M and 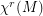 the space of
the space of 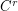 vector fields. There is a dense set
vector fields. There is a dense set 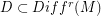 (
(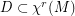 ) such that
) such that 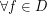 exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space
exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space 
This is a very Deep and Hard problem in Dynamical Systems . It present the dream of the dynamicist mathematicians .
Keywords: Attractors , basins, Finite
Closing Lemma for Diffeomorphism (Dynamical Systems) ★★★★
Author(s): Charles Pugh
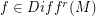 and
and 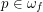 . Then for any neighborhood
. Then for any neighborhood 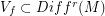 there is
there is 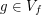 such that
such that  is periodic point of
is periodic point of 
There is an analogous conjecture for flows ( 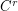 vector fields . In the case of diffeos this was proved by Charles Pugh for
vector fields . In the case of diffeos this was proved by Charles Pugh for 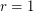 . In the case of Flows this has been solved by Sushei Hayahshy for
. In the case of Flows this has been solved by Sushei Hayahshy for 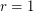 . But in the two cases the problem is wide open for
. But in the two cases the problem is wide open for 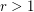
Keywords: Dynamics , Pertubation
Sub-atomic product of funcoids is a categorical product ★★
Author(s):
- \item Product morphism is defined similarly to the category of topological spaces. \item Product object is the sub-atomic product. \item Projections are sub-atomic projections.
See details, exact definitions, and attempted proofs here.
Keywords:
Bounding the on-line choice number in terms of the choice number ★★
Author(s): Zhu
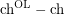 is arbitrarily large?
is arbitrarily large? Keywords: choosability; list coloring; on-line choosability
Are almost all graphs determined by their spectrum? ★★★
Author(s):
Keywords: cospectral; graph invariant; spectrum
Signing a graph to have small magnitude eigenvalues ★★
 is the adjacency matrix of a
is the adjacency matrix of a  -regular graph, then there is a symmetric signing of
-regular graph, then there is a symmetric signing of  (i.e. replace some
(i.e. replace some 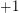 entries by
entries by 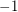 ) so that the resulting matrix has all eigenvalues of magnitude at most
) so that the resulting matrix has all eigenvalues of magnitude at most 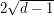 .
. Keywords: eigenvalue; expander; Ramanujan graph; signed graph; signing
The Bollobás-Eldridge-Catlin Conjecture on graph packing ★★★
Author(s):
 and
and  are
are  -vertex graphs and
-vertex graphs and 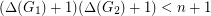 , then
, then  and
and  pack.
pack. Keywords: graph packing
Decomposing k-arc-strong tournament into k spanning strong digraphs ★★
Author(s): Bang-Jensen; Yeo
Keywords:
PTAS for feedback arc set in tournaments ★★
Keywords: feedback arc set; PTAS; tournament
Partitionning a tournament into k-strongly connected subtournaments. ★★
Author(s): Thomassen
 be positve integer Does there exists an integer
be positve integer Does there exists an integer 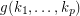 such that every
such that every 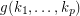 -strong tournament
-strong tournament  admits a partition
admits a partition 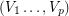 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 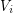 is a non-trivial
is a non-trivial 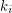 -strong for all
-strong for all 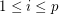 .
. Keywords:
Weighted colouring of hexagonal graphs. ★★
 such that for every hexagonal graph
such that for every hexagonal graph  and vertex weighting
and vertex weighting 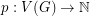 ,
, 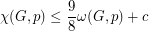
Keywords:
Colouring the square of a planar graph ★★
Author(s): Wegner
 be a planar graph of maximum degree
be a planar graph of maximum degree  . The chromatic number of its square is
. The chromatic number of its square is- \item at most
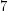 if
if 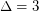 , \item at most
, \item at most 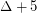 if
if 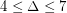 , \item at most
, \item at most 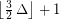 if
if 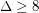 .
. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University