 login/create account
login/create account
Recent Activity
Are there infinite number of Mersenne Primes? ★★★★
Author(s):
![\[ M_n = 2^p - 1 \]](/files/tex/eb18a56e5c2e8b1be6ac733d217c0c1f1a47a94e.png) that is prime.
that is prime.
Are there infinite number of Mersenne Primes?
Keywords: Mersenne number; Mersenne prime
Are all Mersenne Numbers with prime exponent square-free? ★★★
Author(s):
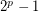 Square free?
Square free? Keywords: Mersenne number
What are hyperfuncoids isomorphic to? ★★
Author(s): Porton
Let 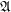 be an indexed family of sets.
be an indexed family of sets.
Products are 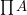 for
for 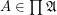 .
.
Hyperfuncoids are filters 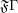 on the lattice
on the lattice 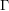 of all finite unions of products.
of all finite unions of products.
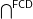 a bijection from hyperfuncoids
a bijection from hyperfuncoids 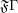 to:
to:- \item prestaroids on
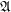 ; \item staroids on
; \item staroids on 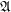 ; \item completary staroids on
; \item completary staroids on 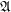 ?
? If yes, is 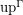 defining the inverse bijection? If not, characterize the image of the function
defining the inverse bijection? If not, characterize the image of the function 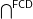 defined on
defined on 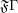 .
.
Consider also the variant of this problem with the set 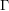 replaced with the set
replaced with the set 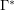 of complements of elements of the set
of complements of elements of the set 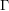 .
.
Keywords: hyperfuncoids; multidimensional
Another conjecture about reloids and funcoids ★★
Author(s): Porton
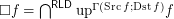 for reloid
for reloid  .
. 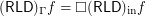 for every funcoid
for every funcoid  .
. Note: it is known that 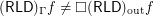 (see below mentioned online article).
(see below mentioned online article).
Keywords:
Inequality for square summable complex series ★★
Author(s): Retkes
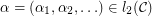 the following inequality holds
the following inequality holds 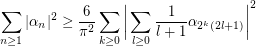
Keywords: Inequality
One-way functions exist ★★★★
Author(s):
Keywords: one way function
Chromatic Number of Common Graphs ★★
Author(s): Hatami; Hladký; Kráľ; Norine; Razborov
Keywords: common graph
Erdős–Straus conjecture ★★
For all 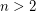 , there exist positive integers
, there exist positive integers  ,
, 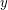 ,
,  such that
such that 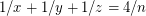 .
.
Keywords: Egyptian fraction
The 3n+1 conjecture ★★★
Author(s): Collatz
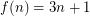 if
if  is odd and
is odd and 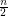 if
if  is even. Let
is even. Let 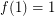 . Assume we start with some number
. Assume we start with some number  and repeatedly take the
and repeatedly take the  of the current number. Prove that no matter what the initial number is we eventually reach
of the current number. Prove that no matter what the initial number is we eventually reach 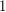 .
. Keywords: integer sequence
List Hadwiger Conjecture ★★
Author(s): Kawarabayashi; Mohar
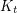 -minor-free graph is
-minor-free graph is 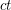 -list-colourable for some constant
-list-colourable for some constant 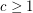 .
. Keywords: Hadwiger conjecture; list colouring; minors
Lucas Numbers Modulo m ★★
Author(s):
Keywords: Lucas numbers
Divisibility of central binomial coefficients ★★
Author(s): Graham
 such that
such that 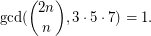
 such that
such that 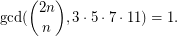
Keywords:
¿Are critical k-forests tight? ★★
Author(s): Strausz
Let  be a
be a  -uniform hypergraph. If
-uniform hypergraph. If  is a critical
is a critical  -forest, then it is a
-forest, then it is a  -tree.
-tree.
Keywords: heterochromatic number
Saturated $k$-Sperner Systems of Minimum Size ★★
Author(s): Morrison; Noel; Scott
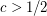 and a function
and a function 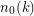 such that if
such that if 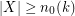 , then every saturated
, then every saturated  -Sperner system
-Sperner system 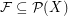 has cardinality at least
has cardinality at least 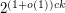 ?
? Keywords: antichain; extremal combinatorics; minimum saturation; saturation; Sperner system
List Colourings of Complete Multipartite Graphs with 2 Big Parts ★★
Author(s): Allagan
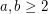 , what is the smallest integer
, what is the smallest integer 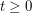 such that
such that 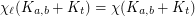 ?
? Keywords: complete bipartite graph; complete multipartite graph; list coloring
Generalised Empty Hexagon Conjecture ★★
Author(s): Wood
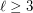 there is an integer
there is an integer 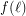 such that every set of at least
such that every set of at least 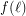 points in the plane contains
points in the plane contains 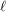 collinear points or an empty hexagon.
collinear points or an empty hexagon. Keywords: empty hexagon
General position subsets ★★
Author(s): Gowers
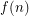 such that every set of at least
such that every set of at least 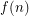 points in the plane contains
points in the plane contains  collinear points or a subset of
collinear points or a subset of  points in general position (no three collinear)?
points in general position (no three collinear)? Forcing a 2-regular minor ★★
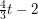 contains every 2-regular graph on
contains every 2-regular graph on  vertices as a minor.
vertices as a minor. Keywords: minors
Fractional Hadwiger ★★
Author(s): Harvey; Reed; Seymour; Wood
 ,
,(a)
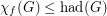
(b)
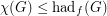
(c)
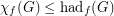 .
. Keywords: fractional coloring, minors
Generalized path-connectedness in proximity spaces ★★
Author(s): Porton
Let  be a proximity.
be a proximity.
A set  is connected regarding
is connected regarding  iff
iff 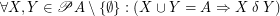 .
.
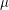 and a set
and a set 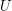 :
:- \item
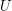 is connected regarding
is connected regarding 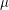 . \item For every
. \item For every 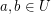 there exists a totally ordered set
there exists a totally ordered set 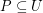 such that
such that 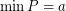 ,
, 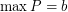 , and for every partion
, and for every partion 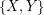 of
of  into two sets
into two sets 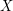 ,
, 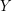 such that
such that 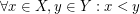 , we have
, we have ![$ X \mathrel{[ \mu]^{\ast}} Y $](/files/tex/0ef560be389646efd1fdde5ebc9afc9ac98ee64e.png) .
. Keywords: connected; connectedness; proximity space

 Drupal
Drupal CSI of Charles University
CSI of Charles University