login/create account
Divisibility of central binomial coefficients
Problem (1) Prove that there exist infinitely many positive integers 
such that 
such that 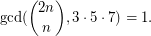Problem (2) Prove that there exists only a finite number of positive integers such that 
such that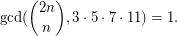
The binomial coefficient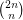 
is not divisible by prime 
iff all the base- digits of are smaller than 
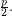
It has been conjectured that 1, 2, 10, 3159, and 3160 are the only positive numbers for which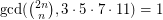 
holds.
Bibliography
." Math. Comp. 29 (1975), 83-92.Sequence A030979: Numbers n such that C(2n,n) is not divisible by 3, 5 or 7.
Andrew Granville. "The Arithmetic Properties of Binomial Coefficients."
* indicates original appearance(s) of problem.
2, 10, and 3159 are not valid for problem (2)
On January 18th, 2012 Anonymous says:
In the initial comment five values are stated to be not divisible by 3, 5, 7, and 11. That is true for 1 and 3160 but not for 2, 10, and 3159:
The last base-3-digit of 2 is 2. The last base-11-digit of 10 is 10. The last base-5-digit 3159 is 4.
Or check these facts:
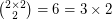
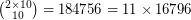
2 and 3159 are not in the sequence A030979 (mentioned in the bibliography).
Reference for problem (2)
On July 23rd, 2012 Ng Yong Hao says:
It appears that the right reference for question 2 should be A151750 instead.
Problem 1 solved?
On March 14th, 2011 tba says:
Looks like Problem 1 was solved by http://arxiv.org/PS_cache/arxiv/pdf/1010/1010.3070v1.pdf
Drupal
CSI of Charles University
It seems Problem (1) was
It seems Problem (1) was solved last year, see http://arxiv.org/abs/1010.3070
How about Problem 2?