 login/create account
login/create account
List Colourings of Complete Multipartite Graphs with 2 Big Parts
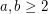 , what is the smallest integer
, what is the smallest integer 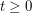 such that
such that 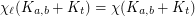 ?
? The list chromatic number of a graph  , denoted
, denoted 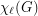 , is the minimum
, is the minimum  such that for every assignment of lists of size
such that for every assignment of lists of size  to the vertices of
to the vertices of  there is a proper colouring in which every vertex is mapped to a colour in its own list. For more background on the list chromatic number, see [3].
there is a proper colouring in which every vertex is mapped to a colour in its own list. For more background on the list chromatic number, see [3].
Given graphs  and
and  , the join of
, the join of  and
and  , denoted
, denoted 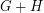 , is obtained by taking disjoint copies of
, is obtained by taking disjoint copies of  and
and  and adding all edges between them. Ohba [1] proved that for every graph
and adding all edges between them. Ohba [1] proved that for every graph  there exists
there exists 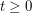 such that
such that 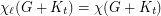 . The question above asks to determine the minimum value of
. The question above asks to determine the minimum value of  in the case that
in the case that  is a complete bipartite graph. It seems that it was first studied in [4], although this is unclear; for the time being, we have chosen to attribute this problem to J. Allagan.
is a complete bipartite graph. It seems that it was first studied in [4], although this is unclear; for the time being, we have chosen to attribute this problem to J. Allagan.
Define 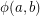 to be the minimum
to be the minimum  such that
such that 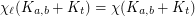 . Note that, if
. Note that, if  is a complete multipartite graph with at most one non-singleton part, then we see that
is a complete multipartite graph with at most one non-singleton part, then we see that 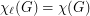 by colouring the vertices of the non-singleton part last. Thus, if
by colouring the vertices of the non-singleton part last. Thus, if  or
or  is equal to 1, then
is equal to 1, then 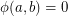 . As it turns out,
. As it turns out, 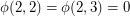 and
and 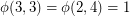 . This can be deduced from the following result of [2] and the fact that
. This can be deduced from the following result of [2] and the fact that 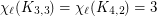 :
:
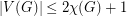 , then
, then 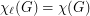 .
. The above result of [2] implies that if 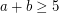 , then
, then 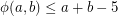 . However it seems that, for most values of
. However it seems that, for most values of 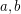 , this bound is far from tight.
, this bound is far from tight.
A simple observation is that, since 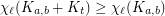 for all
for all  , we must have
, we must have ![\[\phi(a,b)\geq \chi_\ell(K_{a,b}) - \chi(K_{a,b}) = \chi_\ell(K_{a,b}) -2.\]](/files/tex/d269913ffb08a2c6a0ea7e0cf6fa82056124ebf4.png)
The following is a result of Allagan [4]:
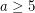 , then
, then ![\[\lfloor \sqrt{a}\rfloor - 1 \leq \phi(a,2)\leq \left\lceil\frac{-7+\sqrt{8a+17}}{2}\right\rceil.\]](/files/tex/d9e6ce2988c5a7ad64ae8cd05c71d9baa3716985.png)
This implies that 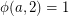 for
for 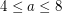 and that
and that 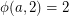 for
for 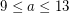 .
.
Bibliography
[1] K. Ohba. On chromatic-choosable graphs, J. Graph Theory. 40 (2002) 130--135. MathSciNet.
[2] J. A. Noel, B. A. Reed, H. Wu. A Proof of a Conjecture of Ohba. Submitted. pdf.
[3] J. A. Noel. Choosability of Graphs with Bounded Order: Ohba's Conjecture and Beyond. Master's Thesis, McGill University. pdf.
[4] J. A. D. Allagan. Choice Numbers, Ohba Numbers and Hall Numbers of some complete  -partite graphs. PhD Thesis. Auburn University. 2009.
-partite graphs. PhD Thesis. Auburn University. 2009.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University