 login/create account
login/create account
Choice Number of k-Chromatic Graphs of Bounded Order
 is a
is a  -chromatic graph on at most
-chromatic graph on at most 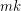 vertices, then
vertices, then 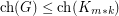 .
.
For integers 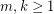 , let
, let  denote the complete
denote the complete  -partite graph in which every part has size
-partite graph in which every part has size  .
.
In one of the original papers on choosability, Erdos, Rubin and Taylor [ERT] proved that 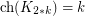 . Later, Ohba [Ohba] conjectured the following generalization: if
. Later, Ohba [Ohba] conjectured the following generalization: if 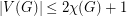 , then TeX Embedding failed!.} This was proved by Noel, Reed and Wu [NRW12].
, then TeX Embedding failed!.} This was proved by Noel, Reed and Wu [NRW12].
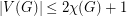 , then
, then 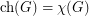 .
. The above theorem implies that the above conjecture holds for 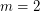 . That is, if
. That is, if  is a
is a  -chromatic graph on at most
-chromatic graph on at most 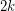 vertices (in fact, at most
vertices (in fact, at most 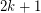 vertices), then
vertices), then 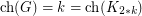 .
.
Kierstead [Kie00] proved that 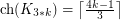 . This was generalized by Noel, West, Wu and Zhu [NWWZ13] to the following:
. This was generalized by Noel, West, Wu and Zhu [NWWZ13] to the following:
 ,
, ![\[\text{ch}(G)\leq\max\left\{\chi(G),\left\lceil\frac{|V(G)|+\chi(G)-1}{3}\right\rceil\right\}.\]](/files/tex/218a69498947f8b282ee7889143ce3a202da78f7.png)
Therefore, if  is a
is a  -chromatic graph on at most
-chromatic graph on at most 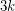 vertices, then
vertices, then 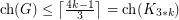 . This shows that the conjecture is true for
. This shows that the conjecture is true for 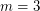 .
.
Recently, Kierstead, Salmon and Wang [KSW14] proved the following:
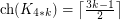 .
. However, it is not known whether the upper bound of 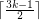 holds for all
holds for all  -chromatic graphs on at most
-chromatic graphs on at most 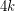 vertices. If true, it would verify the conjecture for
vertices. If true, it would verify the conjecture for 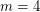 .
.
The following is a refinement of the conjecture.
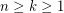 there is a graph
there is a graph 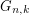 such that
such that- \item
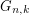 is a complete
is a complete  -partite graph on
-partite graph on  vertices, \item the stability number of
vertices, \item the stability number of 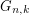 is
is 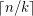 , and \item every
, and \item every  -chromatic graph
-chromatic graph  on at most
on at most  vertices satisfies
vertices satisfies 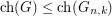 .
. Bibliography
[Alo92] N. Alon. Choice numbers of graphs: a probabilistic approach. Combin. Probab. Comput., 1(2):107–114, 1992.
[ERT80] P. Erdos, A. L. Rubin, and H. Taylor. Choosability in graphs. Congress. Numer., XXVI, pages 125–157, 1980.
[Kie00] H. A. Kierstead. On the choosability of complete multipartite graphs with part size three. Discrete Math., 211(1-3):255–259, 2000.
[KSW14] H. A. Kierstead, A. Salmon and R. Wang. On the Choice Number of Complete Multipartite Graphs With Part Size Four.
*[Noe13] J. A. Noel. Choosability of Graphs With Bounded Order: Ohba's Conjecture and Beyond. Master's thesis, McGill University, Montreal. pdf
[NRW12] J. A. Noel, B. A. Reed, and H. Wu. A Proof of a Conjecture of Ohba. Preprint, arXiv:1211.1999v1, November 2012. Webpage
[NWWZ13] J. A. Noel, D. B. West, H. Wu, and X. Zhu. Beyond Ohba's Conjecture: A bound on the choice number of  -chromatic graphs with
-chromatic graphs with  vertices. Preprint, arXiv:1308.6739v1, August 2013. pdf
vertices. Preprint, arXiv:1308.6739v1, August 2013. pdf
[Ohb02] K. Ohba. On chromatic-choosable graphs. J. Graph Theory, 40(2):130–135, 2002.
[Yan03] D. Yang. Extension of the game coloring number and some results on the choosability of complete multipartite graphs. PhD thesis, Arizona State University, Tempe, Arizona, 2003.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University