 login/create account
login/create account
General position subsets
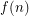 such that every set of at least
such that every set of at least 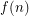 points in the plane contains
points in the plane contains  collinear points or a subset of
collinear points or a subset of  points in general position (no three collinear)?
points in general position (no three collinear)? The 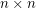 grid contains no set of
grid contains no set of 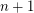 collinear points and no subset of
collinear points and no subset of 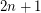 points in general position, implying
points in general position, implying 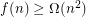 .
.
To see that 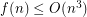 , consider a set
, consider a set  of points that contain no
of points that contain no  collinear points, and contain no subset of
collinear points, and contain no subset of  points in general position. Let
points in general position. Let  be a maximal subset of
be a maximal subset of  in general position. Every point in
in general position. Every point in 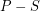 is on one of the
is on one of the 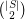 lines determined by
lines determined by  . Each such line contains at most
. Each such line contains at most 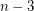 points in
points in 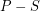 . Thus
. Thus 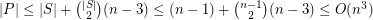 .
.
Payne and Wood [PW] improved this upper bound to 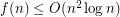 . The proof is based on the Szemerédi-Trotter Theorem and Spencer's Lemma about independent sets in hypergraphs.
. The proof is based on the Szemerédi-Trotter Theorem and Spencer's Lemma about independent sets in hypergraphs.
It is reasonable to think that the grid is the extremal example, and 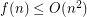 . This would be an elegant generalisation of a result by Erdős [R] who proved that the
. This would be an elegant generalisation of a result by Erdős [R] who proved that the 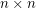 grid contains a subset of
grid contains a subset of 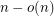 points in general position (the no-three-in-line problem).
points in general position (the no-three-in-line problem).
Bibliography
*[G] Timothy Gowers, A geometric Ramsey problem.
[PW] Michael Payne, David R. Wood. On the general position subset selection problem, SIAM J. Discrete Math. 27.4:1727-1733, 2013.
[R] K. F. Roth, On a problem of Heilbronn, J. London Mathematical Society 26.3:198–204, 1951.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University