Home » Subject » Graph Theory » Hypergraphs

¿Are critical k-forests tight?

Importance: Medium ✭✭
Author(s): Strausz, Ricardo
Subject: Graph Theory
» Hypergraphs
Keywords: heterochromatic number
Recomm. for undergrads: no
Prize: A cognac at Coyoacan
Posted by: Dino
on: September 1st, 2007
Conjecture  

Let $ H $ be a $ k $-uniform hypergraph. If $ H $ is a critical $ k $-forest, then it is a $ k $-tree.

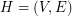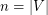We say that a hypergraph $ H=(V,E) $ is a $ k $-graph if it is $ k $-uniform, and denote its order by $ n=|V| $ and its size by $ m=|E| $.

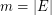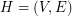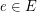Laszlo Lovasz introduced the following concept: a $ k $-graph $ H=(V,E) $ is said to be a $ k $-forest if for every edge $ e\in E $ there exists a $ k $-colouing $ \varsigma\colon V\to[k] $ such that $ \varsigma(e')=[k]\Leftrightarrow e'=e $; that is, such that only the edge $ e $ receives the $ k $ colours in its vertices. Clearly a $ 2 $-forest is simply a forest in the usual sense (i.e., an acyclic graph). Lovasz proved that

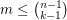Theorem   A $ k $-forest has size at most $ m\leq{n-1\choose k-1} $.

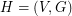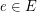On the other hand, Victor Neumann-Lara introduced the following invariant: the heterochromatic number of a $ k $-graph $ H=(V,G) $ is the minimum number of colours $ c $ such that, in every colouring $ \varsigma\colon V\to[c] $ there is an edge wich receives different colours in each of its vertices; that is, there exists $ e\in E $ such that 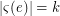$ |\varsigma(e)|=k $. If the heterochromatic number and the rank are equal, the hypergraph is said to be tight. Clearly a 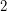$ 2 $-graph is tight if and only if it is connected. A tight $ k $-forest is called a $ k $-tree.

I can prove the following

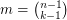Theorem   If a $ k $-forest has size $ m={n-1\choose k-1} $ then it is tight — and therefore a $ k $-tree.

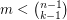Finally, we say that a $ k $-forest is critical if no edge can be added to it without loosing the property of being a $ k $-forest; it is maximal (in size) with such a property. Observe that there are critical $ k $-forests of size $ m<{n-1\choose k-1} $, whenever $ k>2 $.

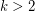So, the conjecture is to motivate the question: ¿are critical $ k $-forests tight?

Bibliography



* indicates original appearance(s) of problem.
add new comment

This has been solved.

On May 5th, 2014 Anonymous says:

See http://arxiv.org/abs/1109.3390

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.