 login/create account
login/create account
Recent Activity
Direct proof of a theorem about compact funcoids ★★
Author(s): Porton
 is a
is a 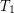 -separable (the same as
-separable (the same as 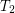 for symmetric transitive) compact funcoid and
for symmetric transitive) compact funcoid and  is a uniform space (reflexive, symmetric, and transitive endoreloid) such that
is a uniform space (reflexive, symmetric, and transitive endoreloid) such that 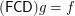 . Then
. Then 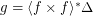 .
. The main purpose here is to find a direct proof of this conjecture. It seems that this conjecture can be derived from the well known theorem about existence of exactly one uniformity on a compact set. But that would be what I call an indirect proof, we need a direct proof instead.
The direct proof may be constructed by correcting all errors an omissions in this draft article.
Direct proof could be better because with it we would get a little more general statement like this:
 be a
be a 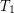 -separable compact reflexive symmetric funcoid and
-separable compact reflexive symmetric funcoid and  be a reloid such that
be a reloid such that- \item
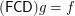 ; \item
; \item 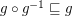 .
. Then 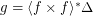 .
.
Keywords: compact space; compact topology; funcoid; reloid; uniform space; uniformity
Dirac's Conjecture ★★
Author(s): Dirac
 of
of  points in the plane, not all collinear, there is a point in
points in the plane, not all collinear, there is a point in  contained in at least
contained in at least 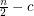 lines determined by
lines determined by  , for some constant
, for some constant  .
. Keywords: point set
Roller Coaster permutations ★★★
Let 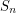 denote the set of all permutations of
denote the set of all permutations of ![$ [n]=\set{1,2,\ldots,n} $](/files/tex/470bd09059264370b76b4da90b77dc370c7e0e7c.png) . Let
. Let 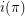 and
and 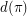 denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in
denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in  . Let
. Let 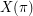 denote the set of subsequences of
denote the set of subsequences of  with length at least three. Let
with length at least three. Let 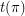 denote
denote 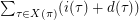 .
.
A permutation 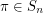 is called a Roller Coaster permutation if
is called a Roller Coaster permutation if 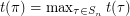 . Let
. Let 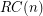 be the set of all Roller Coaster permutations in
be the set of all Roller Coaster permutations in 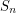 .
.
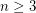 ,
,- \item If
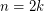 , then
, then 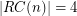 . \item If
. \item If 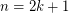 , then
, then 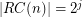 with
with 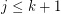 .
. 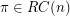 ,
,- \item If
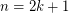 , then
, then 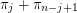 is odd for
is odd for 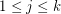 . \item If
. \item If 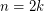 , then
, then 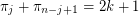 for all
for all 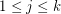 .
. Keywords:
Graphs of exact colorings ★★
Author(s):
Conjecture For 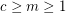 , let
, let 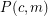 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 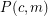 is true if and only if
is true if and only if 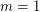 ,
, 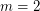 , or
, or  .
.
Keywords:
Imbalance conjecture ★★
Author(s): Kozerenko
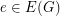 we have
we have 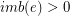 . Then
. Then 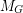 is graphic.
is graphic. Keywords: edge imbalance; graphic sequences
Every metamonovalued reloid is monovalued ★★
Author(s): Porton
Keywords:
Every metamonovalued funcoid is monovalued ★★
Author(s): Porton
The reverse is almost trivial: Every monovalued funcoid is metamonovalued.
Keywords: monovalued
Decomposition of completions of reloids ★★
Author(s): Porton
 and
and  it holds
it holds- \item
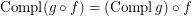 if
if  is a co-complete reloid; \item
is a co-complete reloid; \item 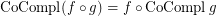 if
if  is a complete reloid; \item
is a complete reloid; \item 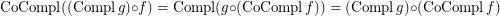 ; \item
; \item 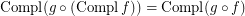 ; \item
; \item 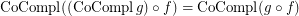 .
. Keywords: co-completion; completion; reloid
List Total Colouring Conjecture ★★
Author(s): Borodin; Kostochka; Woodall
 is the total graph of a multigraph, then
is the total graph of a multigraph, then 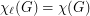 .
. Keywords: list coloring; Total coloring; total graphs
Partitioning the Projective Plane ★★
Author(s): Noel
Throughout this post, by projective plane we mean the set of all lines through the origin in 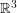 .
.
 of the projective plane is octahedral if all lines in
of the projective plane is octahedral if all lines in  pass through the closure of two opposite faces of a regular octahedron centered at the origin.
pass through the closure of two opposite faces of a regular octahedron centered at the origin.  of the projective plane is weakly octahedral if every set
of the projective plane is weakly octahedral if every set 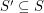 such that
such that 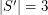 is octahedral.
is octahedral. 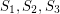 and
and 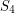 such that each set
such that each set 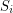 is weakly octahedral. Then each
is weakly octahedral. Then each 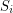 is octahedral.
is octahedral. Keywords: Partitioning; projective plane
Kriesell's Conjecture ★★
Author(s): Kriesell
 be a graph and let
be a graph and let 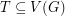 such that for any pair
such that for any pair 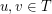 there are
there are 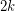 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains  .
. Keywords: Disjoint paths; edge-connectivity; spanning trees
2-colouring a graph without a monochromatic maximum clique ★★
 is a non-empty graph containing no induced odd cycle of length at least
is a non-empty graph containing no induced odd cycle of length at least  , then there is a
, then there is a  -vertex colouring of
-vertex colouring of  in which no maximum clique is monochromatic.
in which no maximum clique is monochromatic. Keywords: maximum clique; Partitioning
Almost all non-Hamiltonian 3-regular graphs are 1-connected ★★
Author(s): Haythorpe
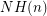 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 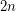 , and similarly denote by
, and similarly denote by 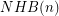 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 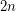 .
.
Is it true that 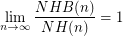 ?
?
Erdős–Faber–Lovász conjecture ★★★
Author(s): Erdos; Faber; Lovasz
 is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
. Keywords: chromatic number
Are there only finite Fermat Primes? ★★★
Author(s):
![\[ F_n = 2^{2^n } + 1 \]](/files/tex/0da5a50010e4e5df91c0d58080245ece34ec9ca6.png) that is prime. The only known Fermat primes are F_0 =3,F_1=5,F_2=17,F_3 =257 ,F_4=65537 It is unknown if other fermat primes exist.
that is prime. The only known Fermat primes are F_0 =3,F_1=5,F_2=17,F_3 =257 ,F_4=65537 It is unknown if other fermat primes exist.
Keywords:
Are all Fermat Numbers square-free? ★★★
Author(s):
![\[ F_n = 2^{2^{n } } + 1 \]](/files/tex/70ca73d7e82af2fee084a8417e172c58cf78b376.png) Square-Free?
Square-Free?
Keywords:
Choosability of Graph Powers ★★
Author(s): Noel
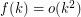 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
Keywords: choosability; chromatic number; list coloring; square of a graph
Erdős-Posa property for long directed cycles ★★
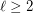 be an integer. For every integer
be an integer. For every integer 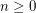 , there exists an integer
, there exists an integer 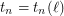 such that for every digraph
such that for every digraph  , either
, either  has a
has a  pairwise-disjoint directed cycles of length at least
pairwise-disjoint directed cycles of length at least 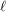 , or there exists a set
, or there exists a set  of at most
of at most 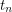 vertices such that
vertices such that 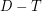 has no directed cycles of length at least
has no directed cycles of length at least 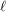 .
. Keywords:
Large acyclic induced subdigraph in a planar oriented graph. ★★
Author(s): Harutyunyan
 has an acyclic induced subdigraph of order at least
has an acyclic induced subdigraph of order at least 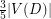 .
. Keywords:
Polignac's Conjecture ★★★
Author(s): de Polignac
In particular, this implies:

 Drupal
Drupal CSI of Charles University
CSI of Charles University