 login/create account
login/create account
Lovasz, Laszlo
Erdős–Faber–Lovász conjecture ★★★
Author(s): Erdos; Faber; Lovasz
Conjecture If  is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
.
 is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
. Keywords: chromatic number
Lovász Path Removal Conjecture ★★
Author(s): Lovasz
Conjecture There is an integer-valued function 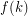 such that if
such that if  is any
is any 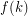 -connected graph and
-connected graph and  and
and 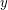 are any two vertices of
are any two vertices of  , then there exists an induced path
, then there exists an induced path  with ends
with ends  and
and 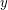 such that
such that 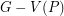 is
is  -connected.
-connected.
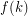 such that if
such that if  is any
is any 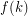 -connected graph and
-connected graph and  and
and 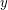 are any two vertices of
are any two vertices of  , then there exists an induced path
, then there exists an induced path  with ends
with ends  and
and 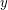 such that
such that 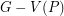 is
is  -connected.
-connected. Keywords:
Double-critical graph conjecture ★★
A connected simple graph  is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
is called double-critical, if removing any pair of adjacent vertexes lowers the chromatic number by two.
Conjecture  is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph
 is the only
is the only  -chromatic double-critical graph
-chromatic double-critical graph Keywords: coloring; complete graph
Exponentially many perfect matchings in cubic graphs ★★★
Conjecture There exists a fixed constant  so that every
so that every  -vertex cubic graph without a cut-edge has at least
-vertex cubic graph without a cut-edge has at least 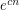 perfect matchings.
perfect matchings.
 so that every
so that every  -vertex cubic graph without a cut-edge has at least
-vertex cubic graph without a cut-edge has at least 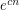 perfect matchings.
perfect matchings. Keywords: cubic; perfect matching
Hamiltonian paths and cycles in vertex transitive graphs ★★★
Author(s): Lovasz
Problem Does every connected vertex-transitive graph have a Hamiltonian path?
Keywords: cycle; hamiltonian; path; vertex-transitive

 Drupal
Drupal CSI of Charles University
CSI of Charles University