Home » Subject » Graph Theory » Directed Graphs
Importance: Medium ✭✭
Author(s): Harutyunyan, Ararat
Subject: Graph Theory
» Directed Graphs
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: June 25th, 2013
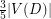Conjecture   Every planar oriented graph $ D $ has an acyclic induced subdigraph of order at least $ \frac{3}{5} |V(D)| $.

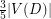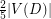Borodin's 5-Colour Theorem states that every planar graph has an acyclic 5-colouring This implies that every planar oriented graph $ D $ has an acyclic induced subdigraph of order at least $ \frac{2}{5} |V(D)| $.

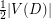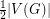Already improving this bound to $ \frac{1}{2} |V(D)| $ would be interesting: it is a relaxtion of both a Conjecture of Albertson and Berman stating that every planar graph $ G $ has an induced forest of order $ \frac{1}{2} |V(G)| $ and a Conjecture of Neumann-Lara stating that every planar oriented graph can be split into two acyclic subdigraphs.

If true, this conjecture would be best possible.

Related problems

Large induced forest in a planar graph.
The Two Color Conjecture

Bibliography



* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options