 login/create account
login/create account
Conjecture Let  be a graph and let
be a graph and let 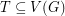 such that for any pair
such that for any pair 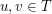 there are
there are 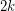 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains 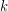 edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains 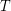 .
.
 be a graph and let
be a graph and let 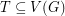 such that for any pair
such that for any pair 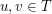 there are
there are 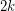 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains 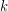 edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains 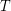 .
. This problem was featured as unsolved problem #22 in Bondy and Murty's book "Graph Theory" [BM].
See also a posting on the open problem forum of the Egerváry Research Group on Combinatorial Optimization.
Bibliography
[BM] J. A. Bondy and U. S. R. Murty. Graph theory, volume 244 of Graduate Texts in Mathematics. Springer, New York, 2008.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University