 login/create account
login/create account
List Total Colouring Conjecture
 is the total graph of a multigraph, then
is the total graph of a multigraph, then 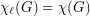 .
.
The list chromatic number of a graph  , denoted
, denoted 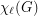 , is defined here. Given a multigraph
, is defined here. Given a multigraph  , the total graph
, the total graph 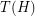 of
of  is a graph on vertex set
is a graph on vertex set 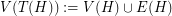 where
where
- \item two elements of
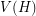 are adjacent in
are adjacent in 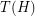 if and only if they are adjacent in
if and only if they are adjacent in  ; \item two elements of
; \item two elements of 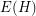 are adjacent in
are adjacent in 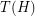 if and only if they share an endpoint; \item an element of
if and only if they share an endpoint; \item an element of 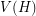 is adjacent to an element of
is adjacent to an element of 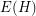 in
in 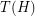 if it is incident with it.
if it is incident with it. This problem is related to the List (Edge) Colouring Conjecture as well as the Total Colouring Conjecture.
Kostochka and Woodall [KW] conjectured that 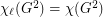 for every graph
for every graph  ; this was known as the List Square Colouring Conjecture. It is stronger than the List Total Colouring Conjecture since, given a multigraph
; this was known as the List Square Colouring Conjecture. It is stronger than the List Total Colouring Conjecture since, given a multigraph  , the total graph of
, the total graph of  can be obtained by subdividing each edge of
can be obtained by subdividing each edge of  and taking the square. Moreover, the graph obtained from
and taking the square. Moreover, the graph obtained from  by subdividing each edge is bipartite and one part of the bipartition consists of vertices of degree
by subdividing each edge is bipartite and one part of the bipartition consists of vertices of degree 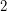 . Thus, the List Total Colouring Conjecture corresponds to this (very) special case of the List Square Colouring Conjecture.
. Thus, the List Total Colouring Conjecture corresponds to this (very) special case of the List Square Colouring Conjecture.
However, the List Square Colouring Conjecture is not true in general. For a family of counterexamples, see the paper of Kim and Park [KP].
Bibliography
*[BKW] O. V. Borodin, A. V. Kostochka, and D. R. Woodall. List edge and list totalcolourings of multigraphs. J. Combin. Theory Ser. B, 71(2):184–204, 1997.
[KW] A. V. Kostochka and D. R. Woodall. Choosability conjectures and multicircuits. Discrete Math., 240(1-3):123–143, 2001.
[KP] Seog-Jin Kim and Boram Park: Counterexamples to the List Square Coloring Conjecture, submitted.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University