 login/create account
login/create account
co-completion
Decomposition of completions of reloids ★★
Author(s): Porton
Conjecture For composable reloids  and
and  it holds
it holds
 and
and  it holds
it holds- \item
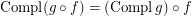 if
if  is a co-complete reloid; \item
is a co-complete reloid; \item 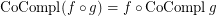 if
if  is a complete reloid; \item
is a complete reloid; \item 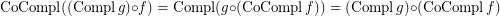 ; \item
; \item 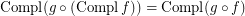 ; \item
; \item 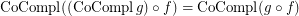 .
. Keywords: co-completion; completion; reloid

 Drupal
Drupal CSI of Charles University
CSI of Charles University