Home » Subject » Combinatorics » Posets
Importance: Medium ✭✭
Author(s): Morrison, Natasha
Noel, Jonathan A.
Scott, Alex
Subject: Combinatorics
» Posets
Keywords: antichain
extremal combinatorics
minimum saturation
saturation
Sperner system
Recomm. for undergrads: yes
Posted by: Jon Noel
on: April 12th, 2014
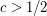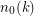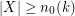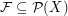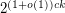Question   Does there exist a constant $ c>1/2 $ and a function $ n_0(k) $ such that if $ |X|\geq n_0(k) $, then every saturated $ k $-Sperner system $ \mathcal{F}\subseteq \mathcal{P}(X) $ has cardinality at least $ 2^{(1+o(1))ck} $?

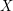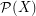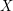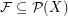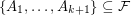The power set of a set $ X $, denoted $ \mathcal{P}(X) $, is the collection of all subsets of $ X $. A collection $ \mathcal{F}\subseteq\mathcal{P}(X) $ is said to be a $ k $-Sperner system if there does not exist a subcollection $ \{A_1,\dots,A_{k+1}\}\subseteq \mathcal{F} $ such that 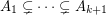$ A_1\subsetneq \dots\subsetneq A_{k+1} $; such a subcollection is called a 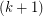$ (k+1) $-chain. 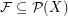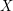A $ k $-Sperner system $ \mathcal{F}\subseteq\mathcal{P}(X) $ is said to be saturated if for every subset $ S $ of $ X $ not contained in 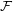$ \mathcal{F} $, the collection 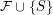$ \mathcal{F}\cup\{S\} $ contains a 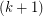$ (k+1) $-chain.

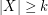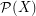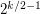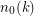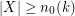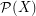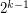Gerbner et al. [1] proved that if $ |X|\geq k $, then every saturated $ k $-Sperner System in $ \mathcal{P}(X) $ has cardinality at least $ 2^{k/2-1} $. Moreover, they conjectured that there exists a function $ n_0(k) $ such that if $ |X|\geq n_0(k) $, then the minimum size of a saturated $ k $-Sperner System in $ \mathcal{P}(X) $ has size $ 2^{k-1} $. This was disproved by Morrison, Noel and Scott in [2], who showed the following:

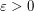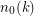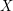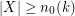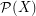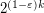Theorem  (Morrison, Noel and Scott (2014))   There exists a constant $ \varepsilon>0 $ and a function $ n_0(k) $ such that for every $ k $ and every set $ X $ such that $ |X|\geq n_0(k) $ there exists a saturated $ k $-Sperner system in $ \mathcal{P}(X) $ of cardinality at most $ 2^{(1-\varepsilon)k} $.

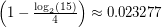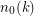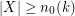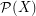The value of $ \varepsilon $ which can be deduced from their proof is approximately $ \left(1-\frac{\log_2(15)}{4}\right)\approx 0.023277 $. Moreover, in [2] it was shown that there exists a function $ n_0(k) $ and a constant $ c\in [1/2,1-\varepsilon] $ such that if $ |X|\geq n_0(k) $, then the size of the smallest $ k $-Sperner System in $ \mathcal{P}(X) $ is asymptotically 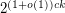$ 2^{(1+o(1))ck} $. The problem stated here is to determine whether $ c>1/2 $.

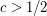A 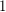$ 1 $-Sperner system is called an antichain. As was observed in [2], a positive answer to the above question would follow from a positive answer to the following question:

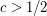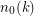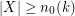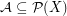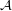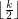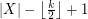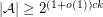Question  (Morrison, Noel, Scott (2014))   Does there exist a constant $ c>1/2 $ and a function $ n_0(k) $ such that if $ |X|\geq n_0(k) $ and $ \mathcal{A}\subseteq\mathcal{P}(X) $ is a saturated antichain in which every element of $ \mathcal{A} $ has cardinality between $ \left\lfloor\frac{k}{2}\right\rfloor $ and $ |X|-\left\lfloor\frac{k}{2}\right\rfloor +1 $, then $ |\mathcal{A}|\geq 2^{(1+o(1))ck} $?

A more general problem is the following:

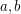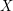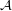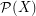Question   Given integers $ a,b $ and a set $ X $, what is the minimum size of a saturated antichain $ \mathcal{A} $ in $ \mathcal{P}(X) $ in which every set of 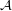$ \mathcal{A} $ has cardinality between $ a $ and $ |X|-b $?

Related problems

Saturation in the Hypercube

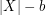Bibliography

[1] D. Gerbner, B. Keszegh, N. Lemons, C. Palmer, D. Palvolgyi, and B. Patkos, Saturating Sperner Families, Graphs Combin. 29 (2013), no. 5, 1355–1364. arXiv:1105.4453

*[2] N. Morrison, J. A. Noel, A. Scott. On Saturated k-Sperner Systems. arXiv:1402.5646 (2014). arXiv:1402.5646


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options