Home » Subject » Graph Theory » Directed Graphs » Tournaments
Importance: Medium ✭✭
Author(s): Bang-Jensen, Joergen
Yeo, Anders
Subject: Graph Theory
» Directed Graphs
» » Tournaments
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: March 15th, 2013
Conjecture   Every k-arc-strong tournament decomposes into k spanning strong digraphs.

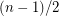Conjecture 8 implies Kelly's conjecture (Every regular tournament of order $ n $ can be decomposed into $ (n-1)/2 $ Hamilton directed cycles.) which has been proved for tournaments of sufficiently large order by Kühn and Osthus [KO].

Bang-Jensen and Yeo [BY] gave several results supporting this conjecture. For example they proved it for $ k $-arc-strong tournaments with minimum in- and out-degree at least $ 37k $.

Related problems

Arc-disjoint strongly connected spanning subdigraphs

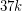Bibliography

*[BY] J. Bang-Jensen, A. Yeo, Decomposing k-arc-strong tournaments into strong spanning subdigraphs, Combinatorica 24 (2004) 331–349.

[KO] Daniela Kühn and Deryk Osthus, Hamilton decompositions of regular expanders: a proof of Kelly's conjecture for large tournaments, Advances in Mathematics 237 (2013), 62-146.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options