 login/create account
login/create account
 and
and  are
are  -vertex graphs and
-vertex graphs and 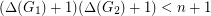 , then
, then  and
and  pack.
pack.
A pair of  -vertex graphs
-vertex graphs  and
and  are said to
are said to 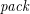 if they are edge-disjoint subgraphs of the complete graph on
if they are edge-disjoint subgraphs of the complete graph on  vertices.
vertices.
The main conjecture in the area of graph packing is the abovementioned conjecture by Bollobás, Eldridge [BE] and Catlin [C].
In support of the BEC-conjecture, Sauer and Spencer [SS] proved that if  and
and  are
are  -vertex graphs and
-vertex graphs and 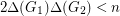 then
then  and
and  pack.
pack.
Given a graph  ,
, 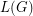 denotes the line graph of
denotes the line graph of  and
and 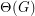 denotes the number
denotes the number 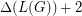 . Kostochka and Yu [KY1] proved that if
. Kostochka and Yu [KY1] proved that if  and
and  are two
are two  -vertex graphs with
-vertex graphs with 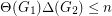 , then
, then  and
and  pack with the following exceptions: (1)
pack with the following exceptions: (1)  is a perfect matching and
is a perfect matching and  is either
is either 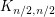 with
with 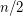 odd or contains
odd or contains 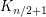 or (2)
or (2)  is a perfect matching and
is a perfect matching and  is
is 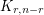 with
with  odd or contains
odd or contains 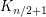 .
.
Kostachka and Yu [KY2] conjectured that if  and
and  are
are  -vertex graphs with
-vertex graphs with 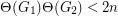 then
then  and
and  pack.
pack.
Bibliography
*[BE] B. Bollabás and S. E. Eldridge, Maximal matchings in graphs with given maximal and minimal degrees, Congr. Numer. XV (1976), 165--168.
*[C] P. A. Catlin, Embedding subgraphs and coloring graphs under extremal degree conditions, Ph. D. Thesis, Ohio State Univ., Columbus (1976).
[KY1] A. V. Kostochka and G. Yu, An Ore-type analogue of the Sauer-Spencer Theorem, Graphs Combin. 23 (2007), 419--424.
[KY2] A. V. Kostochka and G. Yu, An Ore-type graph packing problems, Combin. Probab. Comput. 16 (2007), 167--169.
[SS] N. Sauer and J. Spencer, Edge disjoint placement of graphs, J. Combin. Theory Ser. B 25 (1978), 295--302.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University