 login/create account
login/create account
Subgroup formed by elements of order dividing n
Suppose  is a finite group, and
is a finite group, and  is a positive integer dividing
is a positive integer dividing 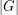 . Suppose that
. Suppose that  has exactly
has exactly  solutions to
solutions to 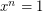 . Does it follow that these solutions form a subgroup of
. Does it follow that these solutions form a subgroup of  ?
?
If these solutions form a subgroup, they form a characteristic (and therefore normal) subgroup of  . This easily follows from the First Sylow Theorem if
. This easily follows from the First Sylow Theorem if  is the highest power of a prime
is the highest power of a prime  dividing
dividing 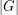 .
.
In a 1980 article, Feit commented that the case where 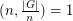 (i.e.,
(i.e.,  'exactly divides'
'exactly divides' 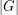 ) had been reduced to considering
) had been reduced to considering  simple. Thus it should be resolvable using the classification of finite simple groups.
simple. Thus it should be resolvable using the classification of finite simple groups.
It is known that if  divides
divides 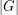 , the number of solutions of
, the number of solutions of 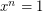 in
in  is a multiple of
is a multiple of  . A generalization of this theorem, replacing
. A generalization of this theorem, replacing 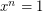 by
by 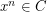 for a conjugacy class
for a conjugacy class  of
of  , can be found in Marshall Hall Jr.'s book.
, can be found in Marshall Hall Jr.'s book.
 is a finite transitive permutation group in which only the identity has more than one fixed point, then the derangements of
is a finite transitive permutation group in which only the identity has more than one fixed point, then the derangements of  , together with the identity, form a subgroup of
, together with the identity, form a subgroup of  .
. To prove Frobenius' Theorem from this (say  is such a permutation group on
is such a permutation group on  points), use the standard elementary counting arguments to show that the solutions to
points), use the standard elementary counting arguments to show that the solutions to 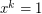 are only the derangements and the identity and that there are exactly
are only the derangements and the identity and that there are exactly  of these. This theorem of Frobenius has not yet been proven in general without the use of group characters.
of these. This theorem of Frobenius has not yet been proven in general without the use of group characters.
Bibliography
Marshall Hall Jr., Theory of Groups, Macmillan (1959)
Walter Feit, On a Conjecture of Frobenius, Proceedings of the American Mathematical Society, Vol.7, No. 2 (Apr. 1956), 177-187.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Solved... again
it can be proved by a isomorphism between the solutions of x^n=1 in G and the solutions of the same eq in C (complex numbers).