 login/create account
login/create account
A nowhere-zero point in a linear mapping ★★★
Author(s): Jaeger
Conjecture If 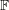 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 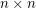 matrix with entries in
matrix with entries in 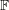 , then there are column vectors
, then there are column vectors 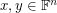 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 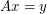 .
.
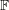 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 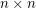 matrix with entries in
matrix with entries in 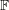 , then there are column vectors
, then there are column vectors 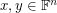 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 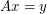 .
. Keywords: invertible; nowhere-zero flow
Partitioning edge-connectivity ★★
Author(s): DeVos
Question Let  be an
be an 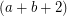 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 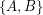 of
of 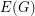 so that
so that 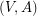 is
is  -edge-connected and
-edge-connected and 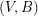 is
is  -edge-connected?
-edge-connected?
 be an
be an 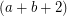 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 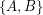 of
of 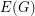 so that
so that 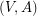 is
is  -edge-connected and
-edge-connected and 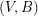 is
is  -edge-connected?
-edge-connected? Keywords: edge-coloring; edge-connectivity
Acyclic edge-colouring ★★
Author(s): Fiamcik
Conjecture Every simple graph with maximum degree 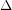 has a proper
has a proper 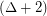 -edge-colouring so that every cycle contains edges of at least three distinct colours.
-edge-colouring so that every cycle contains edges of at least three distinct colours.
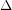 has a proper
has a proper 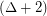 -edge-colouring so that every cycle contains edges of at least three distinct colours.
-edge-colouring so that every cycle contains edges of at least three distinct colours. Keywords: edge-coloring
Packing T-joins ★★
Author(s): DeVos
Conjecture There exists a fixed constant  (probably
(probably 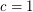 suffices) so that every graft with minimum
suffices) so that every graft with minimum  -cut size at least
-cut size at least  contains a
contains a  -join packing of size at least
-join packing of size at least 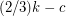 .
.
 (probably
(probably 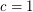 suffices) so that every graft with minimum
suffices) so that every graft with minimum  -cut size at least
-cut size at least  contains a
contains a  -join packing of size at least
-join packing of size at least 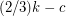 .
. The Berge-Fulkerson conjecture ★★★★
Conjecture If  is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 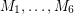 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 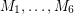 .
.
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 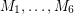 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 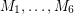 .
.
Keywords: cubic; perfect matching
Decomposing eulerian graphs ★★★
Author(s):
Conjecture If  is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and  is a 2-transition system for
is a 2-transition system for  , then
, then 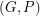 has a compaible decomposition.
has a compaible decomposition.
 is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and  is a 2-transition system for
is a 2-transition system for  , then
, then 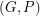 has a compaible decomposition.
has a compaible decomposition. Faithful cycle covers ★★★
Author(s): Seymour
Conjecture If 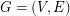 is a graph,
is a graph, 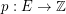 is admissable, and
is admissable, and 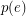 is even for every
is even for every 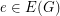 , then
, then 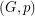 has a faithful cover.
has a faithful cover.
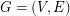 is a graph,
is a graph, 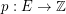 is admissable, and
is admissable, and 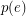 is even for every
is even for every 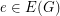 , then
, then 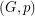 has a faithful cover.
has a faithful cover. (m,n)-cycle covers ★★★
Author(s): Celmins; Preissmann
Conjecture Every bridgeless graph has a (5,2)-cycle-cover.

 Drupal
Drupal CSI of Charles University
CSI of Charles University