Home » Subject » Graph Theory » Coloring » Edge coloring

Petersen coloring conjecture

Importance: High ✭✭✭
Author(s): Jaeger, Francois
Subject: Graph Theory
» Coloring
» » Edge coloring
Keywords: cubic
edge-coloring
Petersen graph
Recomm. for undergrads: no
Prize: none
Posted by: mdevos
on: March 7th, 2007
Conjecture   Let $ G $ be a cubic graph with no bridge. Then there is a coloring of the edges of $ G $ using the edges of the Petersen graph so that any three mutually adjacent edges of $ G $ map to three mutually adjancent edges in the Petersen graph.

This extrordainary conjecture asserts that in a very strong sense, every bridgeless cubic graph has all of the cycle-space properties posessed by the Petersen graph. If true, this conjecture would imply both The Berge-Fulkerson conjecture and The five cycle double cover conjecture.

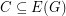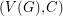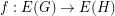If $ G $ is a graph and $ C \subseteq E(G) $ we say that $ C $ is a binary cycle if every vertex in the graph $ (V(G),C) $ has even degree. If $ H $ is a graph and $ f : E(G) \rightarrow E(H) $ is a map, we say that $ f $ is cycle-continuous if the pre-image of every binary cycle is a binary cycle. The following conjecture is an equivalent reformulation of the Petersen coloring conjecture.

Conjecture  (Petersen coloring conjecture (2))   Every bridgeless graph has a cycle-continuous mapping to the Petersen graph.
add new comment

Question

On November 8th, 2011 Anonymous says:

For which bridgeless cubic graphs has this been checked for?

reply

Re:

On November 24th, 2011 Robert Samal says:

It is trivially true for all that are 3-edge-colorable -- which is the vast majority. Among the rest, I checked it using computer and lists of snarks for all graphs upto 34 vertices. (And some more -- e.g. all flower-snarks.)

Best wishes, Robert

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.