Home » Subject » Graph Theory » Coloring » Edge coloring
Importance: High ✭✭✭
Author(s): Jaeger, Francois
Subject: Graph Theory
» Coloring
» » Edge coloring
Keywords: cubic
edge-coloring
Petersen graph
Recomm. for undergrads: no
Prize: none
Posted by: mdevos
on: March 7th, 2007
Conjecture   Let $ G $ be a cubic graph with no bridge. Then there is a coloring of the edges of $ G $ using the edges of the Petersen graph so that any three mutually adjacent edges of $ G $ map to three mutually adjancent edges in the Petersen graph.

This extrordainary conjecture asserts that in a very strong sense, every bridgeless cubic graph has all of the cycle-space properties posessed by the Petersen graph. If true, this conjecture would imply both The Berge-Fulkerson conjecture and The five cycle double cover conjecture.

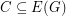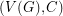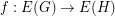If $ G $ is a graph and $ C \subseteq E(G) $ we say that $ C $ is a binary cycle if every vertex in the graph $ (V(G),C) $ has even degree. If $ H $ is a graph and $ f : E(G) \rightarrow E(H) $ is a map, we say that $ f $ is cycle-continuous if the pre-image of every binary cycle is a binary cycle. The following conjecture is an equivalent reformulation of the Petersen coloring conjecture.

Conjecture  (Petersen coloring conjecture (2))   Every bridgeless graph has a cycle-continuous mapping to the Petersen graph.
2 comments

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options