Graph Theory » Directed Graphs

Woodall's Conjecture ★★★

Author(s): Woodall

Conjecture   If $ G $ is a directed graph with smallest directed cut of size $ k $, then $ G $ has $ k $ disjoint dijoins.

Keywords: digraph; packing

Posted by mdevos
updated April 5th, 2007
add new comment
Graph Theory » Topological G.T. » Coloring

Grunbaum's Conjecture ★★★

Author(s): Grunbaum

Conjecture   If $ G $ is a simple loopless triangulation of an orientable surface, then the dual of $ G $ is 3-edge-colorable.

Keywords: coloring; surface

Posted by mdevos
updated March 23rd, 2009
5 comments

Trivia

Here is a little trivia about our website:
  • The symmetry group of the Dodecahedron (our icon) is the smallest group which is not solvable

Philosophy

We view our website as serving a role complementary to that of Wikipedia and to the websites designed to distribute research papers (MathSciNet, the Archive, and scholarly search tools such as Google Search). Whereas these tools provide an excellent service in giving researchers access to established knowledge, we hope to provide a forum for discussion and exploration of the frontier.

As such, we have no desire to recreate these other services. We hope our users post their preprints on the archive - where we will link to them, and we hope our users utilize the already impressive collection of mathematical definitions in Wikipedia (both by learning from them, and improving them). Instead of providing our own bibliography pages, we link to online copies of papers and to MathSciNet, and instead of forming our own definitions pages, we prefer that our users build Wikipedia - our \Def command provides a Wikipedia link (see guidelines for details).

read more
Graph Theory » Topological G.T. » Genus

Consecutive non-orientable embedding obstructions ★★★

Author(s):

Conjecture   Is there a graph $ G $ that is a minor-minimal obstruction for two non-orientable surfaces?

Keywords: minor; surface

Posted by Bruce Richter
updated September 15th, 2010
2 comments
Graph Theory » Coloring » Vertex coloring

Strong colorability ★★★

Author(s): Aharoni; Alon; Haxell

Let $ r $ be a positive integer. We say that a graph $ G $ is strongly $ r $-colorable if for every partition of the vertices to sets of size at most $ r $ there is a proper $ r $-coloring of $ G $ in which the vertices in each set of the partition have distinct colors.

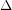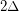Conjecture   If $ \Delta $ is the maximal degree of a graph $ G $, then $ G $ is strongly $ 2 \Delta $-colorable.

Keywords: strong coloring

Posted by berger
updated November 19th, 2009
5 comments
Graph Theory » Coloring

Linial-Berge path partition duality ★★★

Author(s): Berge; Linial

Conjecture   The minimum $ k $-norm of a path partition on a directed graph $ D $ is no more than the maximal size of an induced $ k $-colorable subgraph.

Keywords: coloring; directed path; partition

Posted by berger
updated September 19th, 2007
2 comments