 login/create account
login/create account
The Two Color Conjecture ★★
Author(s): Neumann-Lara
Conjecture If  is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 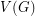 into
into 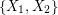 so that the graph induced by
so that the graph induced by 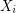 is acyclic for
is acyclic for 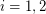 .
.
 is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 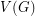 into
into 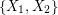 so that the graph induced by
so that the graph induced by 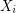 is acyclic for
is acyclic for 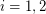 .
. Pentagon problem ★★★
Author(s): Nesetril
Question Let  be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than  . Is it true that for large enough~
. Is it true that for large enough~ there is a homomorphism
there is a homomorphism 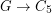 ?
?
 be a 3-regular graph that contains no cycle of length shorter than
be a 3-regular graph that contains no cycle of length shorter than  . Is it true that for large enough~
. Is it true that for large enough~ there is a homomorphism
there is a homomorphism 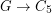 ?
? Keywords: cubic; homomorphism
Ryser's conjecture ★★★
Author(s): Ryser
Conjecture Let  be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 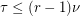 .
.
 be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 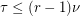 .
. Keywords: hypergraph; matching; packing
Graham's conjecture on tree reconstruction ★★
Author(s): Graham
Problem for every graph  , we let
, we let 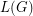 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 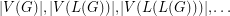 ?
?
 , we let
, we let 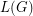 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 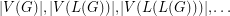 ?
? Keywords: reconstruction; tree
Subset-sums equality (pigeonhole version) ★★★
Author(s):
Problem Let 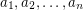 be natural numbers with
be natural numbers with 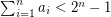 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 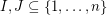 with
with 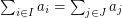 . Is it possible to find such a pair
. Is it possible to find such a pair 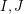 in polynomial time?
in polynomial time?
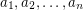 be natural numbers with
be natural numbers with 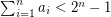 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 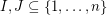 with
with 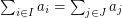 . Is it possible to find such a pair
. Is it possible to find such a pair 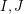 in polynomial time?
in polynomial time? Keywords: polynomial algorithm; search problem
The Erdös-Hajnal Conjecture ★★★
Conjecture For every fixed graph  , there exists a constant
, there exists a constant 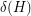 , so that every graph
, so that every graph  without an induced subgraph isomorphic to
without an induced subgraph isomorphic to  contains either a clique or an independent set of size
contains either a clique or an independent set of size 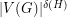 .
.
 , there exists a constant
, there exists a constant 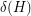 , so that every graph
, so that every graph  without an induced subgraph isomorphic to
without an induced subgraph isomorphic to  contains either a clique or an independent set of size
contains either a clique or an independent set of size 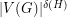 .
. Keywords: induced subgraph
Hamiltonian paths and cycles in vertex transitive graphs ★★★
Author(s): Lovasz
Problem Does every connected vertex-transitive graph have a Hamiltonian path?
Keywords: cycle; hamiltonian; path; vertex-transitive
57-regular Moore graph? ★★★
Keywords: cage; Moore graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University