 login/create account
login/create account
matching
Strong matchings and covers ★★★
Author(s): Aharoni
Let  be a hypergraph. A strongly maximal matching is a matching
be a hypergraph. A strongly maximal matching is a matching 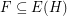 so that
so that 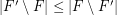 for every matching
for every matching 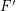 . A strongly minimal cover is a (vertex) cover
. A strongly minimal cover is a (vertex) cover 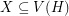 so that
so that 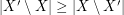 for every cover
for every cover 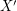 .
.
Conjecture If  is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 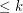 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover.
 is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 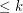 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover. Keywords: cover; infinite graph; matching
Matchings extend to Hamiltonian cycles in hypercubes ★★
Keywords: Hamiltonian cycle; hypercube; matching
Ryser's conjecture ★★★
Author(s): Ryser
Conjecture Let  be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 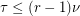 .
.
 be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 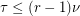 .
. Keywords: hypergraph; matching; packing

 Drupal
Drupal CSI of Charles University
CSI of Charles University