 login/create account
login/create account
Let  be a hypergraph. A strongly maximal matching is a matching
be a hypergraph. A strongly maximal matching is a matching 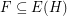 so that
so that 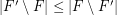 for every matching
for every matching 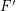 . A strongly minimal cover is a (vertex) cover
. A strongly minimal cover is a (vertex) cover 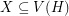 so that
so that 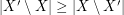 for every cover
for every cover 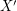 .
.
 is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 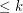 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover. The theory of matching in finite graphs is quite well understood. Now, thanks to the work of Aharoni and others, much of this theory has been extended to infinite graphs. On the other hand, matching in hypergraphs - both finite and infinite - is a subject where our knowledge apears to be lacking. The above conjecture asserts a rather basic property of hypergraphs which would be nice to verify.
This conjecture is (of course) trivial for finite hypergraphs, but it looks very difficult for infinite ones. It has been proved by Aharoni [A2] for the case when 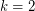 , that is, for infinite graphs. Here the key tool is an infinite version of the Tutte-Edmonds-Gallai decomposition theorem [A1].
, that is, for infinite graphs. Here the key tool is an infinite version of the Tutte-Edmonds-Gallai decomposition theorem [A1].
Next we offer another interesting conjecture of Aharoni on minimal covers.
 is a (possibly infinite) graph and
is a (possibly infinite) graph and  is the hypergraph of independent sets in
is the hypergraph of independent sets in  , then
, then  has a strongly minimal cover.
has a strongly minimal cover. Bibliography
[A1] R. Aharoni, Matchings in infinite graphs. J. Combin. Theory Ser. B 44 (1988), no. 1, 87--125. MathSciNet.
*[A2] R. Aharoni, Infinite matching theory. Directions in infinite graph theory and combinatorics (Cambridge, 1989). Discrete Math. 95 (1991), no. 1-3, 5--22. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University