 login/create account
login/create account
 be an
be an  -uniform
-uniform  -partite hypergraph. If
-partite hypergraph. If  is the maximum number of pairwise disjoint edges in
is the maximum number of pairwise disjoint edges in  , and
, and  is the size of the smallest set of vertices which meets every edge, then
is the size of the smallest set of vertices which meets every edge, then 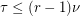 .
. Definitions: A (vertex) cover is a set of vertices which meets (has nonempty intersection with) every edge, and we let 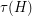 denote the size of the smallest vertex cover of
denote the size of the smallest vertex cover of  . A matching is a collection of pairwise disjoint edges, and we let
. A matching is a collection of pairwise disjoint edges, and we let 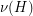 denote the size of the largest matching in
denote the size of the largest matching in  . When the hypergraph is clear from context, we just write
. When the hypergraph is clear from context, we just write  or
or  .
.
It is immediate that 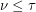 , since every cover must contain at least one point from each edge in any matching. For
, since every cover must contain at least one point from each edge in any matching. For  -uniform hypergraphs,
-uniform hypergraphs, 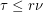 , since the union of the edges from any maximal matching is a set of at most
, since the union of the edges from any maximal matching is a set of at most  vertices that which meets every edge. Ryser's conjecture is that this second bound can be improved if
vertices that which meets every edge. Ryser's conjecture is that this second bound can be improved if  is
is  -uniform and
-uniform and  -partite (the vertices may be partitioned into
-partite (the vertices may be partitioned into  sets
sets 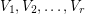 so that every edge contains exactly one element of each
so that every edge contains exactly one element of each 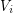 ).
).
In the special case when 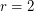 our trivial inequality yields
our trivial inequality yields 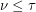 and the conjecture implies
and the conjecture implies 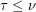 , so we should have
, so we should have  . In fact this is true, it is König's theorem on bipartite graphs [K]. Indeed, Ryser's conjecture is probably easiest to view as a high dimensional generalization of this early result of König. Recently, Aharoni [A] has applied the "Hall's theorem for hypergraphs" result of Aharoni and Haxell [AH] to prove this conjecture for
. In fact this is true, it is König's theorem on bipartite graphs [K]. Indeed, Ryser's conjecture is probably easiest to view as a high dimensional generalization of this early result of König. Recently, Aharoni [A] has applied the "Hall's theorem for hypergraphs" result of Aharoni and Haxell [AH] to prove this conjecture for 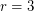 . However the case
. However the case 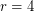 is still wide open.
is still wide open.
Some other interesting work on this problem concerns fractional covers and fractional matchings. A fractional cover of 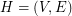 is a weighting
is a weighting 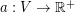 so that
so that 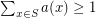 for every
for every 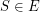 , and the weight of this cover is
, and the weight of this cover is 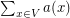 . The fractional cover number, denoted
. The fractional cover number, denoted 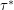 is the infimum of the set of weights of covers. Similarly, a fractional matching is an edge-weighting
is the infimum of the set of weights of covers. Similarly, a fractional matching is an edge-weighting 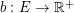 so that
so that 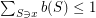 for every
for every 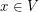 , and the weight of this matching is
, and the weight of this matching is 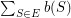 . The fractional matching number, denoted
. The fractional matching number, denoted 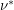 is the supremum of the set of weights of fractional matchings. Fractional covers and matchings are the usual fractional relaxations, and by LP-duality, they satisfy
is the supremum of the set of weights of fractional matchings. Fractional covers and matchings are the usual fractional relaxations, and by LP-duality, they satisfy 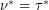 for every hypergraph. For
for every hypergraph. For  -regular
-regular  -partite hypergraphs, Füredi [F] has proved that
-partite hypergraphs, Füredi [F] has proved that 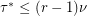 and Lovasz [L] has shown
and Lovasz [L] has shown 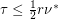 .
.
Bibliography
[A] R. Aharoni, Ryser's conjecture for tripartite 3-graphs. Combinatorica 21 (2001), no. 1, 1--4. MathSciNet
[AH] R. Aharoni and P. Haxell, Hall's theorem for hypergraphs. J. Graph Theory 35 (2000), no. 2, 83--88. MathSciNet
[F] Z. Füredi, Maximum degree and fractional matchings in uniform hypergraphs, Combinatorica 1 (1981), 155--162. MathSciNet
[K] D. König, Theorie der endlichen und unendlichen Graphen, Leipzig, 1936.
[L] L. Lovász, On minimax theorems of combinatorics, Ph.D thesis, Matemathikai Lapok 26 (1975), 209--264 (in Hungarian). MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University