 login/create account
login/create account
search problem
Subset-sums equality (pigeonhole version) ★★★
Author(s):
Problem Let 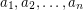 be natural numbers with
be natural numbers with 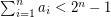 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 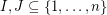 with
with 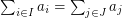 . Is it possible to find such a pair
. Is it possible to find such a pair 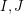 in polynomial time?
in polynomial time?
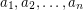 be natural numbers with
be natural numbers with 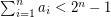 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 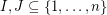 with
with 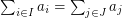 . Is it possible to find such a pair
. Is it possible to find such a pair 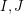 in polynomial time?
in polynomial time? Keywords: polynomial algorithm; search problem

 Drupal
Drupal CSI of Charles University
CSI of Charles University