Open Problem Garden

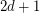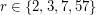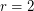A Moore graph is a graph with diameter and girth . It is known that every Moore graph is regular [S] (even distance-regular), and two (rather trivial) families of such graphs are provided by complete graphs and odd cycles. In one of the founding papers in the subject of algebraic graph theory, Hoffman and Singleton [HS] proved that every -regular Moore graph with diameter 2 must have . For and 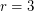such graphs exist, are unique, and are familiar: the pentagon, and the Petersen graph. For 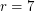Hoffman and Singleton constructed such a graph - now known as the Hoffman-Singleton graph, but for 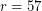we are still uncertain whether such a graph exists.

The pentagon, the Petersen graph, and the Hoffman-Singleton graph are all very highly symmetric graphs, and much of the interest in these objects is related to exceptional phenomena in small finite groups. In contrast to this, Higman proved that a 57-regular Moore graph cannot be vertex transitive (see [C]). In some sense, this is indication that even if a 57-regular Moore graph exists, it will be of less interest than its younger siblings. Nevertheless, as a lingering problem left by one of the first papers in algebraic graph theory, this is viewed as an important question.

There are some easily established properties of a 57-regular Moore graph. For instance it must have 3250 vertices and independence number at most 400. However it seems not nearly enough is known to narrow the search sufficiently.